
(本小题满分12分)已知函数 ,
, .
.
(1)证明: ;
;
(2)若 在
在 恒成立,求
恒成立,求 的最小值.
的最小值.
(1)详见解析;(2)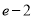 .
.
【解析】
试题分析:(1)求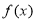 的导数,判断
的导数,判断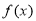 在
在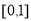 上的单调性,从而可求函数的最小值,即可证明不等式成立;(2)令
上的单调性,从而可求函数的最小值,即可证明不等式成立;(2)令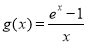 ,可知
,可知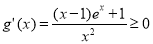 ,从而
,从而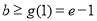 ,而
,而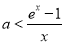 等价于
等价于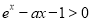 在
在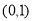 上恒成立,分类讨论,即可求得实数
上恒成立,分类讨论,即可求得实数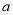 的取值范围.
的取值范围.
试题解析:(1)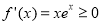 ,即
,即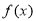 在
在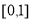 上单调递增,∴
上单调递增,∴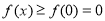 ,即结论成立; (2)令
,即结论成立; (2)令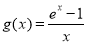 ,则
,则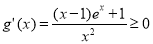 ,
,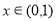 ,∴当
,∴当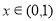 时,
时,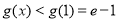 ,要使
,要使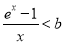 ,只需
,只需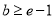 ,要使
,要使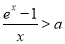 成立,只需
成立,只需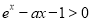 在
在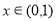 恒成立,令
恒成立,令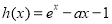 ,
,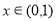 ,则
,则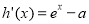 ,由
,由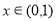 ,
,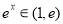 ,①当
,①当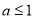 时,
时,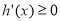 ,此时
,此时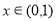 ,有
,有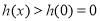 成立,∴
成立,∴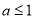 满足条件,②当
满足条件,②当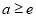 时,
时,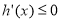 ,此时
,此时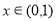 ,有
,有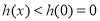 ,不符合题意,舍去,③当
,不符合题意,舍去,③当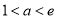 时,令
时,令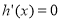 ,得
,得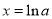 ,可得当
,可得当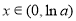 时,
时,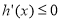 ,即
,即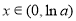 时,
时,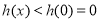 ,不符合题意,舍去,综上,
,不符合题意,舍去,综上,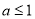 ,又∵
,又∵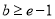 ,
,
∴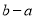 的最小值为
的最小值为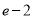 .
.
考点:1.利用导数求函数在闭区间上的最值;2.恒成立问题;3.分类讨论的数学思想.
考点分析: 考点1:导数及其应用 试题属性

科目:高中数学 来源:2014-2015学年江苏省常州市高三上学期期末调研测试文科数学试卷(解析版) 题型:解答题
(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为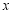 (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为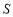 (m2).
(m2).
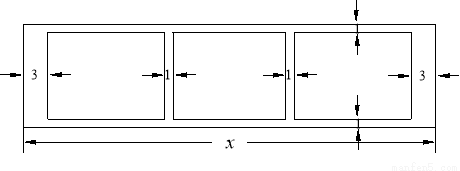
(1)求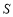 关于
关于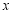 的函数关系式;
的函数关系式;
(2)求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省龙岩市非一级达标校高三上学期期末检查文科数学试卷(解析版) 题型:填空题
若不等式组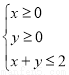 所表示的平面区域被直线
所表示的平面区域被直线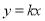 分为面积相等的两部分,则
分为面积相等的两部分,则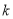 的值是 .
的值是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:解答题
(本小题满分12分)袋子中装有大小相同的白球和红球共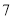 个,从袋子中任取
个,从袋子中任取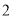 个球都是白球的概率为
个球都是白球的概率为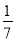 ,每个球被取到的机会均等.现从袋子中每次取
,每个球被取到的机会均等.现从袋子中每次取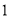 个球,如果取出的是白球则不再放回,设在取得红球之前已取出的白球个数为
个球,如果取出的是白球则不再放回,设在取得红球之前已取出的白球个数为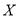 .
.
(1)求袋子中白球的个数;
(2)求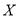 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com