
【题目】设各项均为正数的数列{an}的前n项和为Sn,满足:对任意的n∈N*,都有an+1+Sn+1=1,又a1![]() .
.
(1)求数列{an}的通项公式;
(2)令bn=log2an,求![]() (n∈N*)
(n∈N*)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
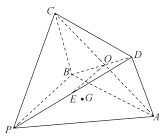
【题目】如图所示的几何体![]() 中,四边形
中,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为平面
为平面![]() 内任一点.
内任一点.
(1)在平面![]() 内,过
内,过![]() 点是否存在直线
点是否存在直线![]() 使
使![]() ?如果不存在,请说明理由,如果存在,请说明作法;
?如果不存在,请说明理由,如果存在,请说明作法;
(2)过![]() ,
, ![]() ,
, ![]() 三点的平面将几何体
三点的平面将几何体![]() 截去三棱锥
截去三棱锥![]() ,求剩余几何体
,求剩余几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再将所得图像上的每个点的横坐标伸长为原来的2倍,纵坐标不变,所得图像关于直线
个单位长度,再将所得图像上的每个点的横坐标伸长为原来的2倍,纵坐标不变,所得图像关于直线![]() 对称,则
对称,则![]() 的最小正值为( )
的最小正值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(a,3),圆C:(x﹣1)2+(y﹣2)2=4.
(1)设a=4,求过点A且与圆C相切的直线方程;
(2)设a=3,直线l过点A且被圆C截得的弦长为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,长半轴长与短半轴长的比值为
,长半轴长与短半轴长的比值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .若点
.若点![]() 在以线段
在以线段![]() 为直径的圆上,求直线
为直径的圆上,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国委员会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制的频率分布直方图如下图所示,把年龄落在区间[15,35)和[35,75]内的人分别称为“青少年人”和“中老年人”.经统计“青少年人”和“中老年人”的人数之比为19:21.其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是2:1.
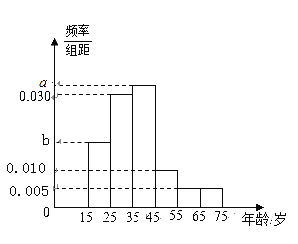
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)现采用分层抽样在[25,35)和[45,55)中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
(Ⅲ)根据已知条件,完成下面的2×2列联表,并根据此统计结果判断:能否有99.9%的把握认为“中老年人”比“青少年人”更加关注“两会”?
关注 | 不关注 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com