
分析 (I)利用等差数列的通项公式列出方程解出公差,代入通项公式即可;
(II)利用通项公式判断{an}的非负项项数,使用求和公式计算.
解答 解:(I)∵a1=10,5a1a3=(2a2+2)2,
∴50(10+2d)=4(10+d+1)2,
即d2-3d-4=0,解得d=-1或d=4.
故an=-n+11或an=4n+6.
(II)由题知d=-1,an=-n+11,则当n≤11时,an≥0,
当n>11时,an<0,
则|a1|+|a2|+|a3|+…+|a2021|=(a1+…+a11)-(a12+…+a2021)
=2(a1+…+a11)-(a1+a2…+a2021)
=2×$\frac{10+0}{2}×11$-$\frac{10-2010}{2}×2021$
=2021110.
点评 本题考查了等差数列的性质,等差数列的前n项和,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | {y|1≤y≤2} | B. | {y|y≥2} | C. | {y|$\frac{1}{2}$≤y≤1} | D. | {y|y≥1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,$\frac{3}{2}$) | B. | [1,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,2) | D. | [$\frac{3}{2}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
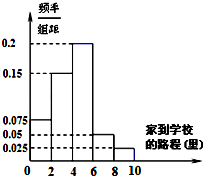 某高中地处市区,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:
某高中地处市区,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:| 下午开始 上课时间 | 2:10 | 2:20 | 2:30 | 2:40 | 2:50 |
| 平均每天 午休人数 | 250 | 350 | 500 | 650 | 750 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 非以上错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com