
| A. | [1,$\frac{3}{2}$) | B. | [1,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,2) | D. | [$\frac{3}{2}$,2] |
分析 通过函数f(x)满足f(x)=3f(x+2)可知函数向右平移2个单位时最大值变为原来的$\frac{1}{3}$,进而可知数列{an}是首项为1、公比为$\frac{1}{3}$的等比数列,计算即得结论.
解答 解::∵函数f(x)满足f(x)=3f(x+2),
∴f(x+2)=$\frac{1}{3}$f(x),即函数向右平移2个单位,最大值变为原来的$\frac{1}{3}$,
又∵当x∈[0,2)时,f(x)=-x2+2x,
∴a1=f(1)=1,
∴数列{an}是首项为1、公比为$\frac{1}{3}$的等比数列,
∴Sn=$\frac{1-(\frac{1}{3})^{n}}{1-\frac{1}{3}}$∈$[1,\frac{3}{2})$.
故选:A.
点评 本题考查了函数图象变换、等比数列的通项公式及其求和公式,考查了推理能力与计算能力,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$ | B. | $\frac{19}{21}$ | C. | $\frac{10}{11}$ | D. | $\frac{11}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
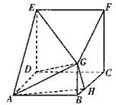 在多面体ABCDEFG中,四边形ABCD与CDEF均为边长为4的正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.
在多面体ABCDEFG中,四边形ABCD与CDEF均为边长为4的正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
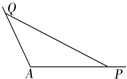 如图,角A为钝角,且sinA=$\frac{3}{5}$,点P、Q分别是在角A的两边上不同于点A的动点.
如图,角A为钝角,且sinA=$\frac{3}{5}$,点P、Q分别是在角A的两边上不同于点A的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | 1 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com