
【题目】已知椭圆![]()
![]() (
(![]() )的离心率为
)的离心率为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上,设与
上,设与![]() 平行的直线
平行的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 分别与
分别与![]() 轴正半轴交于
轴正半轴交于![]() ,
, ![]() 两点.
两点.
(I)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)判断![]() 的值是否为定值,并证明你的结论.
的值是否为定值,并证明你的结论.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)根据椭圆![]() 的离心率为
的离心率为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上,结合性质
上,结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() 、
、![]() ,即可得椭圆
,即可得椭圆![]() 的标准方程;(Ⅱ)由
的标准方程;(Ⅱ)由![]() ,设直线
,设直线![]() (
(![]() )联立方程,
)联立方程, 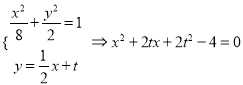 ,根据韦达定理及斜率公式先证明
,根据韦达定理及斜率公式先证明![]()
![]() ,可得直线
,可得直线![]() 和直线
和直线![]() 的斜率和为零,可得
的斜率和为零,可得![]() ,故
,故![]() ,从而得
,从而得![]() 在线段
在线段![]() 的中垂线上,进而可得.
的中垂线上,进而可得.
试题解析:(Ⅰ)由题意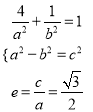 ,
,
解得: ![]() ,
, ![]() ,
, ![]()
故椭圆![]() 的标准方程为
的标准方程为![]()
(Ⅱ)假设直线TP或TQ的斜率不存在,则P点或Q点的坐标为(2,-1),直线l的方程为![]() ,即
,即![]() .
.
联立方程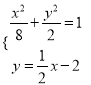 ,得
,得![]() ,
,
此时,直线l与椭圆C相切,不合题意.
故直线TP和TQ的斜率存在.
方法1:
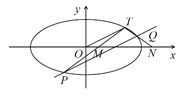
设![]() ,
, ![]() ,则
,则
直线![]() ,,
,,
直线![]()
故![]() ,
, ![]() ,
,
由直线![]() ,设直线
,设直线![]() (
(![]() ),
),
联立方程, 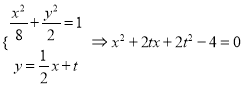 ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
,
![]()
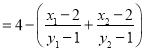
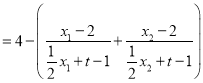
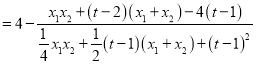
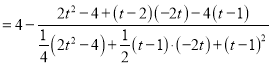
![]() .
.
方法2:
设![]() ,
, ![]() ,直线
,直线![]() 和
和![]() 的斜率分别为
的斜率分别为![]() 和
和![]() ,
,
由![]() ,设直线
,设直线![]() (
(![]() ),
),
联立方程, 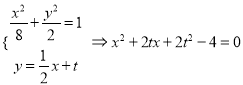 ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
,
![]()
![]()
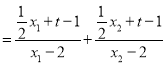
![]()
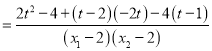 ,
,
![]()
故直线![]() 和直线
和直线![]() 的斜率和为零,
的斜率和为零,
故![]() ,
,
故![]() ,
,
故![]() 在线段
在线段![]() 的中垂线上,即
的中垂线上,即![]() 的中点横坐标为2
的中点横坐标为2
故![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知向量![]() 且函数
且函数![]() ,若函数f(x)的图象上两个相邻的对称轴距离为
,若函数f(x)的图象上两个相邻的对称轴距离为![]() .
.
(1)求函数f(x)的解析式;
(2)将函数y=f(x)的图象向左平移![]() 个单位后,得到函数y=g(x)的图象,求函数g(x)的表达式并其对称轴;
个单位后,得到函数y=g(x)的图象,求函数g(x)的表达式并其对称轴;
(3)若方程f(x)=m(m>0)在![]() 时,有两个不同实数根x1,x2,求实数m的取值范围,并求出x1+x2的值.
时,有两个不同实数根x1,x2,求实数m的取值范围,并求出x1+x2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和椭圆
和椭圆![]() ,
, ![]() 是椭圆
是椭圆![]() 的左焦点.
的左焦点.
(Ⅰ)求椭圆![]() 的离心率和点
的离心率和点![]() 的坐标;
的坐标;
(Ⅱ)点![]() 在椭圆
在椭圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,交圆
轴的垂线,交圆![]() 于点
于点![]() (
(![]() 不重合),
不重合),![]() 是过点
是过点![]() 的圆
的圆![]() 的切线.圆
的切线.圆![]() 的圆心为点
的圆心为点![]() ,半径长为
,半径长为![]() .试判断直线
.试判断直线![]() 与圆
与圆![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.因为运算,数的威力无限;没有运算,数就只是一个符号.对数运算与指数幂运算是两类重要的运算.
(1)对数的运算性质降低了运算的级别,简化了运算,在数学发展史上是伟大的成就.对数运算性质的推导有很多方法.请同学们根据所学知识推导如下的对数运算性质:如果![]() ,且
,且![]() ,
,![]() ,那么
,那么![]() ;
;
(2)请你运用上述对数运算性质计算![]() 的值;
的值;
(3)因为![]() ,所以
,所以![]() 的位数为4(一个自然数数位的个数,叫做位数).请你运用所学过的对数运算的知识,判断
的位数为4(一个自然数数位的个数,叫做位数).请你运用所学过的对数运算的知识,判断![]() 的位数.(注
的位数.(注![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用给人民群众的健康带来了一定的危害.为了给消费者带来放心的蔬菜,某农村合作社每年投入资金![]() 万元,搭建甲、乙两个无公害蔬菜大棚,每个大棚至少要投入资金
万元,搭建甲、乙两个无公害蔬菜大棚,每个大棚至少要投入资金![]() 万元,其中甲大棚种西红柿,乙大棚种黄瓜.根据以往的种菜经验,发现种西红柿的年收入
万元,其中甲大棚种西红柿,乙大棚种黄瓜.根据以往的种菜经验,发现种西红柿的年收入![]() 、种黄瓜的年收入
、种黄瓜的年收入![]() 与各自的资金投入
与各自的资金投入![]() (单位:万元)满足
(单位:万元)满足![]() ,
,![]() .设甲大棚的资金投入为
.设甲大棚的资金投入为![]() (单位:万元),每年两个大棚的总收入为
(单位:万元),每年两个大棚的总收入为![]() (单位:万元).
(单位:万元).
(1)求![]() 的值;
的值;
(2)试问如何安排甲、乙两个大棚的资金投入,才能使总收入![]() 最大.
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法的错误的是( )
A. 经过定点![]() 的倾斜角不为
的倾斜角不为![]() 的直线的方程都可以表示为
的直线的方程都可以表示为![]()
B. 经过定点![]() 的倾斜角不为
的倾斜角不为![]() 的直线的方程都可以表示为
的直线的方程都可以表示为![]()
C. 不经过原点的直线的方程都可以表示为![]()
D. 经过任意两个不同的点![]() 、
、![]() 直线的方程都可以表示为
直线的方程都可以表示为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大连市某企业为确定下一年投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
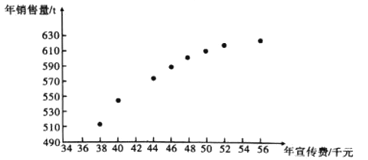
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 573 | 6.8 | 289.8 | 1.6 | 215083.4 | 31280 |
表中![]() ,
,![]() .
.
![]() 根据散点图判断,
根据散点图判断,![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
![]() 根据
根据![]() 的判断结果及表中数据,建立
的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
![]() 已知这种产品的年利润
已知这种产品的年利润![]() 与
与![]() 、
、![]() 的关系为
的关系为![]() .根据
.根据![]() 的结果回答下列问题:
的结果回答下列问题:
![]() 年宣传费
年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
![]() 年宣传费
年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
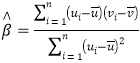 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com