
分析 f(x)=(log2x)?x=$\left\{\begin{array}{l}{xlo{g}_{2}x,x≥1}\\{\frac{lo{g}_{2}x}{x},0<x<1}\end{array}\right.$,及其数列{an}是公比大于0的等比数列,且a6=1,对公比q分类讨论,再利用对数的运算性质即可得出.
解答 解:∵f(x)=(log2x)?x=$\left\{\begin{array}{l}{xlo{g}_{2}x,x≥1}\\{\frac{lo{g}_{2}x}{x},0<x<1}\end{array}\right.$,
∵数列{an}是公比大于0的等比数列,且a6=1,
①1<q时,a1,a2,…,a5∈(0,1),a7,a8,a9,a10∈[1,+∞),${a}_{1}{q}^{5}$=1.
∴${a}_{1}=\frac{1}{{q}^{5}}$,
分别为:$\frac{1}{{q}^{5}}$,$\frac{1}{{q}^{4}}$,…,$\frac{1}{q}$,1,q,…,q4.
∵f(a1)+f(a2)+f(a3)+…+f(a9)+f(a10)=2a1,
∴$\frac{lo{g}_{2}{a}_{1}}{{a}_{1}}$+$\frac{lo{g}_{2}{a}_{2}}{{a}_{2}}$+…+$\frac{lo{g}_{2}{a}_{5}}{{a}_{5}}$+0+a7log2a7+…+a10log2a10=2a1,
∴${q}^{5}lo{g}_{2}\frac{1}{{q}^{5}}$+q4$lo{g}_{2}\frac{1}{{q}^{4}}$+…+$qlo{g}_{2}\frac{1}{q}$+qlog2q+…+${q}^{4}lo{g}_{2}{q}^{4}$=2×$\frac{1}{{q}^{5}}$.
∴${q}^{5}lo{g}_{2}\frac{1}{{q}^{5}}$=2×$\frac{1}{{q}^{5}}$.左边小于0,右边大于0,不成立,舍去.
②0<q<1时,${a}_{1}{q}^{5}$=1,∴${a}_{1}=\frac{1}{{q}^{5}}$,
分别为:$\frac{1}{{q}^{5}}$,$\frac{1}{{q}^{4}}$,…,$\frac{1}{q}$,1,q,…,q4,a1,a2,…,a5∈(1,+∞);a7,a8,a9,a10∈(0,1),
∵f(a1)+f(a2)+f(a3)+…+f(a9)+f(a10)=2a1,
∴$\frac{1}{{q}^{5}}lo{g}_{2}\frac{1}{{q}^{5}}$+$\frac{1}{{q}^{4}}$$lo{g}_{2}\frac{1}{{q}^{4}}$+…+$\frac{1}{q}$$lo{g}_{2}\frac{1}{q}$+$\frac{1}{q}$log2q+…+$\frac{1}{{q}^{4}}lo{g}_{2}{q}^{4}$=2×$\frac{1}{{q}^{5}}$.
∴$\frac{1}{{q}^{5}}lo{g}_{2}\frac{1}{{q}^{5}}$=2×$\frac{1}{{q}^{5}}$.
∴$\frac{1}{{q}^{5}}$=4,
∴a1=4.
③q=1时,a1=…=a6=…=a10=1,不满足f(a1)+f(a2)+f(a3)+…+f(a9)+f(a10)=2a1,舍去.
综上可得:a1=4.
故答案为:4.
点评 本题考查了等比数列的通项公式及其性质、对数的运算性质,考查了分类讨论方法、推理能力与计算能力,属于难题.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | f′(a)<0,f′(b)<0 | B. | f′(a)>0,f′(b)>0 | C. | f′(a)<0,f′(b)>0 | D. | f′(a)>0,f′(b)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
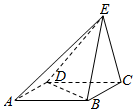 如图ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
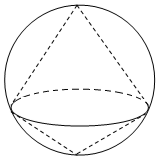 一个透明的球形装饰品内放置了两个公共底面的圆锥如图,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球面面积的$\frac{3}{16}$,则较大圆锥与较小圆锥的体积之比为3:1.
一个透明的球形装饰品内放置了两个公共底面的圆锥如图,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球面面积的$\frac{3}{16}$,则较大圆锥与较小圆锥的体积之比为3:1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
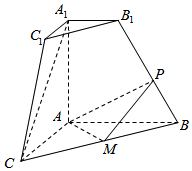 如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2.直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.M为线段BC的中点,P为线段BB1上的动点.
如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2.直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.M为线段BC的中点,P为线段BB1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 圆O上两点C,D在直径AB的两侧(如图甲),沿直径AB将圆O折起形成一个二面角(如图乙),若∠DOB的平分线交弧$\widehat{BD}$于点G,交弦BD于点E,F为线段BC的中点.
圆O上两点C,D在直径AB的两侧(如图甲),沿直径AB将圆O折起形成一个二面角(如图乙),若∠DOB的平分线交弧$\widehat{BD}$于点G,交弦BD于点E,F为线段BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
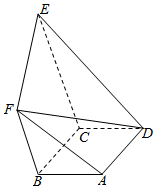 如图,四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BF⊥BC,BF<CE,BF=2,AB=1,AD=$\sqrt{5}$.
如图,四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BF⊥BC,BF<CE,BF=2,AB=1,AD=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2π}{3}$ | B. | -$\frac{π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com