
设函数f(x)=ax-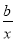 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
(1)求f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
(1)f(x)=x-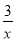
(2)见解析
【解析】【解析】
(1)方程7x-4y-12=0可化为y=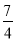 x-3,
x-3,
当x=2时,y=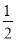 .
.
又f′(x)=a+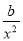 ,
,
于是 ,解得
,解得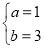
故f(x)=x-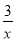 .
.
(2)证明:设P(x0,y0)为曲线上任一点,由f′(x)=1+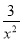 知,曲线在点P(x0,y0)处的切线方程为y-y0=(1+
知,曲线在点P(x0,y0)处的切线方程为y-y0=(1+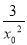 )·(x-x0),即y-(x0-
)·(x-x0),即y-(x0-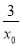 )=(1+
)=(1+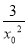 )(x-x0).
)(x-x0).
令x=0得,y=-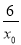 ,从而得切线与直线x=0,交点坐标为(0,-
,从而得切线与直线x=0,交点坐标为(0,-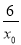 ).
).
令y=x,得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0).
所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为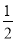 |-
|-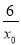 ||2x0|=6.
||2x0|=6.
曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,此定值为6.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-3函数的奇偶性与周期性(解析版) 题型:选择题
若f(x)为奇函数,且在(-∞,0)内是增函数,又f(-2)=0,则xf(x)<0的解集为( )
A.(-2,0)∪(0,2) B.(-∞,-2)∪(0,2)
C.(-∞,-2)∪(2,+∞) D.(-2,0)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-12导数的应用二(解析版) 题型:解答题
已知函数f(x)=x3+ax2+bx+a2(a,b∈R).
(1)若函数f(x)在x=1处有极值10,求b的值;
(2)若对于任意的a∈[-4,+∞),f(x)在x∈[0,2]上单调递增,求b的最小值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-11导数的应用一(解析版) 题型:填空题
已知函数f(x)=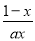 +lnx,若函数f(x)在[1,+∞)上为增函数,则正实数a的取值范围为________.
+lnx,若函数f(x)在[1,+∞)上为增函数,则正实数a的取值范围为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-11导数的应用一(解析版) 题型:选择题
函数f(x)=x2-2lnx的单调递减区间是( )
A.(0,1] B.[1,+∞)
C.(-∞,-1]∪(0,1] D.[-1,0)∪(0,1]
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:填空题
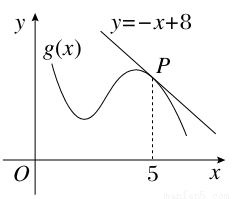
如图,函数g(x)=f(x)+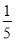 x2的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=________.
x2的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-8n次独立重复实验与二项分布(解析版) 题型:解答题
某工厂生产A,B两种元件,其质量按测试指标划分,指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100个进行检测,检测结果统计如下:
测试 指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
元件A | 8 | 12 | 40 | 32 | 8 |
元件B | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计元件A,元件B为正品的概率;
(2)生产1个元件A,若是正品则盈利40元,若是次品则亏损5元;生产1个元件B,若是正品则盈利50元,若是次品则亏损10元.在(1)的前提下,
(ⅰ)X为生产1个元件A和1个元件B所得的总利润,求随机变量X的分布列和数学期望;
(ⅱ)求生产5个元件B所得利润不少于140元的概率.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:选择题
一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c(a,b,c∈(0,1)),已知他投篮一次得分的均值为2,则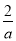 +
+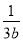 的最小值为( )
的最小值为( )
A.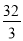 B.
B.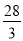 C.
C.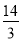 D.
D.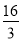
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-5古典概型(解析版) 题型:选择题
连续投掷两次骰子得到的点数分别为m,n,向量a=(m,n)与向量b=(1,0)的夹角记为α,则α∈(0,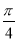 )的概率为( )
)的概率为( )
A.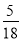 B.
B.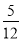 C.
C.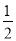 D.
D.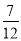
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com