
某工厂生产A,B两种元件,其质量按测试指标划分,指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100个进行检测,检测结果统计如下:
测试 指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
元件A | 8 | 12 | 40 | 32 | 8 |
元件B | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计元件A,元件B为正品的概率;
(2)生产1个元件A,若是正品则盈利40元,若是次品则亏损5元;生产1个元件B,若是正品则盈利50元,若是次品则亏损10元.在(1)的前提下,
(ⅰ)X为生产1个元件A和1个元件B所得的总利润,求随机变量X的分布列和数学期望;
(ⅱ)求生产5个元件B所得利润不少于140元的概率.
(1)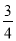
(2)(ⅰ) 随机变量X的分布列为
X | 90 | 45 | 30 | -15 |
P |
|
|
|
|
数学期望E(X)=66
(ⅱ) 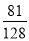
【解析】(1)由题意知,元件A为正品的概率约为 =
=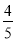 .
.
元件B为正品的概率约为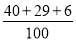 =
=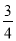 .
.
(2)(ⅰ)随机变量X的所有可能取值为90,45,30,-15.
P(X=90)=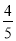 ×
×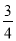 =
=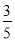 ;
;
P(X=45)= ×
× =
=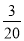 ;
;
P(X=30)=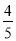 ×
×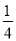 =
= ;
;
P(X=-15)= ×
×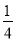 =
=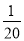 .
.
所以,随机变量X的分布列为
X | 90 | 45 | 30 | -15 |
P |
|
|
|
|
数学期望E(X)=90×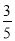 +45×
+45×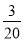 +30×
+30× +(-15)×
+(-15)× =66.
=66.
(ⅱ)设生产的5个元件B中正品有n个,则次品有(5-n)个.
依题意,得50n-10(5-n)≥140,解得n≥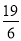 ,
,
所以n=4或n=5.
设“生产5个元件B所得利润不少于140元”为事件A,
则P(A)= (
( )4×
)4×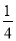 +(
+( )5=
)5=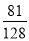 .
.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-2函数的单调性与最值(解析版) 题型:填空题
设函数f(x)的图象关于y轴对称,又已知f(x)在(0,+∞)上为减函数,且f(1)=0,则不等式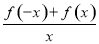 <0的解集为________.
<0的解集为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:解答题
设函数f(x)=ax-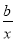 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
(1)求f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:选择题
已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)<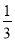 ,则f(x)<
,则f(x)<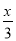 +
+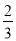 的解集为( )
的解集为( )
A.{x|-1<x<1} B.{x|x<-1}
C.{x|x<-1或x>1} D.{x|x>1}
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-8n次独立重复实验与二项分布(解析版) 题型:填空题
抛掷红、蓝两颗骰子,设事件A为“蓝色骰子的点数为3或6”,事件B为“两颗骰子的点数之和大于8”.当已知蓝色骰子的点数为3或6时,则两颗骰子的点数之和大于8的概率为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-8n次独立重复实验与二项分布(解析版) 题型:选择题
已知随机变量X服从二项分布,X~B(6,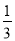 ),则P(X=2)等于( )
),则P(X=2)等于( )
A.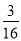 B.
B.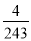 C.
C.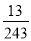 D.
D.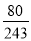
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-6几何概型(解析版) 题型:解答题
在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有6人.
(1)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现从中随机抽取2人上台抽奖,求a和b至少有一人上台抽奖的概率;
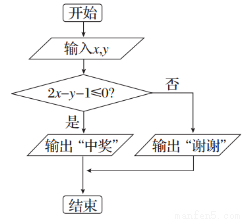
(2)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖.求该代表中奖的概率.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-4随机事件的概率(解析版) 题型:选择题
甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,其中a,b∈{0,1,2,3},若|a-b|≤1,则称甲、乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )
A.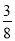 B.
B. C.
C.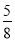 D.
D.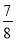
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com