
分析 (1)由f(x)=$\frac{4^x}{{{4^x}+{2}}}$,x∈R.利用函数性质能推导出对一切实数x,f(x)+f(1-x)恒为定值1.
(2)由f(x)+f(1-x)=1,能示出f(-6)+f(-5)+f(-4)+f(-3)+…+f(0)+…+f(6)+f(7)的值.
解答 证明:(1)∵f(x)=$\frac{4^x}{{{4^x}+{2}}}$,x∈R.
∴对一切实数x,
f(x)+f(1-x)=$\frac{{4}^{x}}{{4}^{x}+{2}^{\;}}$+$\frac{{4}^{1-x}}{{4}^{1-x}+{2}^{\;}}$
=$\frac{{4}^{x}}{{4}^{x}+{2}^{\;}}+\frac{4}{4+2•{4}^{x}}$=$\frac{4^x}{{{4^x}+{2}}}$+$\frac{2}{2+{4}^{x}}$=1,
∴对一切实数x,f(x)+f(1-x)恒为定值1.
解:(2)∵f(x)+f(1-x)=1,
∴f(-6)+f(-5)+f(-4)+f(-3)+…+f(0)+…+f(6)+f(7)
=[f(-6)+f(7)]+[f(-5)+f(6)]+[f(-4)+f(5)]+[f(-3)+f(4)]
+[f(-2)+f(3)]+[f(-1)+f(2)]+[f(0)+f(1)]
=1+1+1+1+1+1+1=7.
点评 本题考查函数值的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x-1,g(x)=$\frac{x^2}{x}$-1 | B. | f(x)=2x-1,g(x)=2x+1 | ||
| C. | f(x)=x2,g(x)=$\root{3}{{x}^{6}}$ | D. | f(x)=1,g(x)=x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
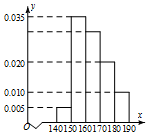 某高三年级有500名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),若在身高[160,170),[170,180),[180,190]三组内的学生中,用分层抽样的方法选取30人参加一项活动,则从身高在[160,170)内的学生中选取的人数应为15.
某高三年级有500名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),若在身高[160,170),[170,180),[180,190]三组内的学生中,用分层抽样的方法选取30人参加一项活动,则从身高在[160,170)内的学生中选取的人数应为15.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
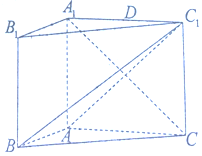 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1是矩形,∠BAC=90°,AA1⊥BC,AA1=AC=2AB=4,且BC1⊥A1C
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1是矩形,∠BAC=90°,AA1⊥BC,AA1=AC=2AB=4,且BC1⊥A1C查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com