
【题目】如图,在三棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点.
中点.
(1)求证: ![]() ;
;
(2)求二面角![]() 的大小.
的大小.

【答案】(1)证明见解析;(2)60°.
【解析】试题分析:
(1)连结PD,由题意可得![]() ,则AB⊥平面PDE,
,则AB⊥平面PDE, ![]() ;
;
(2)法一:结合几何关系做出二面角的平面角,计算可得其正切值为![]() ,故二面角的
,故二面角的![]() 大小为
大小为![]() ;
;
法二:以D为原点建立空间直角坐标系,计算可得平面PBE的法向量![]() .平面PAB的法向量为
.平面PAB的法向量为![]() .据此计算可得二面角的
.据此计算可得二面角的![]() 大小为
大小为![]() .
.
试题解析:
(1)连结PD,![]() PA=PB,
PA=PB,![]() PD
PD![]() AB.
AB.![]()
![]() ,BC
,BC![]() AB,DE
AB,DE![]() AB.
AB.
又![]()
![]() ,
,![]() AB
AB![]() 平面PDE,
平面PDE,![]() PE平面PDE,
PE平面PDE,
∴AB![]() PE.
PE.
(2)法一:
![]() 平面PAB
平面PAB![]() 平面ABC
平面ABC![]() 平面ABC=AB,PD
平面ABC=AB,PD![]() AB,PD
AB,PD![]() 平面ABC.
平面ABC.
则DE![]() PD,又ED
PD,又ED![]() AB,PD
AB,PD![]() 平面AB=D,DE
平面AB=D,DE![]() 平面PAB,
平面PAB,
过D做DF垂直PB与F,连接EF,则EF![]() PB,∠DFE为所求二面角的平面角,
PB,∠DFE为所求二面角的平面角,
则:DE=![]() ,DF=
,DF=![]() ,则
,则![]() ,故二面角的
,故二面角的![]() 大小为
大小为![]()
法二:
![]() 平面PAB
平面PAB![]() 平面ABC,平面PAB
平面ABC,平面PAB![]() 平面ABC=AB,PD
平面ABC=AB,PD![]() AB,PD
AB,PD![]() 平面ABC.
平面ABC.
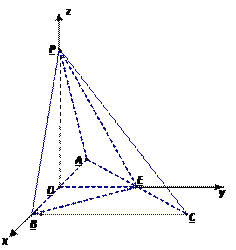
如图,以D为原点建立空间直角坐标系,
![]() B(1,0,0),P(0,0,
B(1,0,0),P(0,0,![]() ),E(0,
),E(0, ![]() ,0),
,0),
![]()
![]() =(1,0,
=(1,0, ![]() ),
), ![]() =(0,
=(0, ![]() ,
, ![]() ).
).
设平面PBE的法向量![]() ,
,
![]()
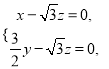 令
令![]() ,得
,得![]() .
.
![]() DE
DE![]() 平面PAB,
平面PAB, ![]() 平面PAB的法向量为
平面PAB的法向量为![]() .
.
设二面角的![]() 大小为
大小为![]() ,由图知,
,由图知, 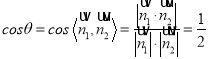 ,
,
所以![]() 即二面角的
即二面角的![]() 大小为
大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数y=f(x)的定义域为R,并且满足f(x+y)=f(x)+f(y),f(![]() )=1,当x>0时,f(x)>0.
)=1,当x>0时,f(x)>0.
(1)求f(0)的值;
(2)判断函数的奇偶性;
(3)如果f(x)+f(2+x)<2,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线 ![]() (a>0,b>0)的左右焦点分别为F1 , F2渐近线分别为l1 , l2 , 位于第一象限的点P在l1上,若l2⊥PF1 , l2∥PF2 , 则双曲线的离心率是( )
(a>0,b>0)的左右焦点分别为F1 , F2渐近线分别为l1 , l2 , 位于第一象限的点P在l1上,若l2⊥PF1 , l2∥PF2 , 则双曲线的离心率是( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月1日起全国统一实施全面两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取70后和80后作为调查对象,随机调查了100位,得到数据如表:
生二胎 | 不生二胎 | 合计 | |
70后 | 30 | 15 | 45 |
80后 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
(1)以这100个人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中随机抽取3位,记其中生二胎的人数为X,求随机变量X的分布列和数学期望;
(2)根据调查数据,是否有90%以上的把握认为“生二胎与年龄有关”,并说明理由.
参考数据:
P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱中ABC﹣A1B1C1中,点A1在平面ABC内的射影D为棱AC的中点,侧面A1ACC1为边长为2的菱形,AC⊥CB,BC=1. 
(1)证明:AC1⊥平面A1BC;
(2)求二面角B﹣A1C﹣B1的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆锥曲线C的极坐标方程为p2= ![]() ,定点A(0,﹣
,定点A(0,﹣ ![]() ),F1 , F2是圆锥曲线C的左、右焦点,直线l经过点F1且平行于直线AF2 .
),F1 , F2是圆锥曲线C的左、右焦点,直线l经过点F1且平行于直线AF2 .
(1)求圆锥曲线C的直角坐标方程和直线l的参数方程;
(2)若直线l与圆锥曲线C交于M,N两点,求|F1M||F1N|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥C的底面是正方形,PA⊥平面ABCD,PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点.

(1)求证:AF∥平面PEC
(2)求证:平面PCD⊥平面PEC;
(3)求三棱锥C-BEP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示几何体ABC﹣A1B1C1中,A1、B1、C1在面ABC上的射影分别是线段AB、BC、AC的中点,面A1B1C1∥面ABC,△ABC是边长为2的等边三角形. 
(1)求证:△A1B1C1是等边三角形;
(2)若面ACB1A1⊥面BA1B1 , 求该几何体ABC﹣A1B1C1的体积;
(3)在(2)的条件下,求面ABC与面A1B1B所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com