
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
已知函数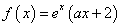 (
( 为自然对数的底数,
为自然对数的底数,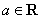 为常数).对于函数
为常数).对于函数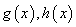 ,若存在常数
,若存在常数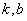 ,对于任意
,对于任意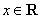 ,不等式
,不等式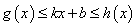 都成立,则称直线
都成立,则称直线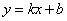 是函数
是函数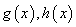 的分界线.
的分界线.
(Ⅰ)若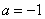 ,求
,求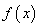 的极值;
的极值;
(Ⅱ)讨论函数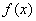 的单调性;
的单调性;
(Ⅲ)设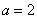 ,试探究函数
,试探究函数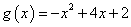 与函数
与函数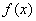 是否存在“分界线”?若存在,求出分界线方程;若不存在,试说明理由.
是否存在“分界线”?若存在,求出分界线方程;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
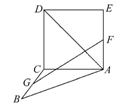
如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为( )
A. 
 B.
B. 
 C.
C. 
 D.
D. 

查看答案和解析>>
科目:高中数学 来源: 题型:
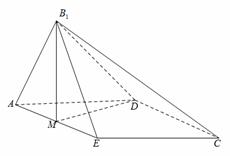
如图,已知等腰梯形 中,
中,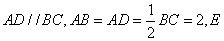 是
是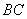 的中点,
的中点,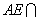
 ,将
,将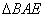 沿着
沿着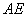 翻折成
翻折成 ,使平面
,使平面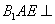 平面
平面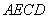 .
.
(I) 求证: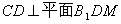 ;
;
(II)求二面角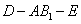 的余弦值;
的余弦值;
(III)在线段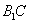 上是否存在点P,使得
上是否存在点P,使得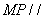 平面
平面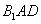 ,若存在,求出
,若存在,求出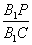 的值;若不存在,说明理由.
的值;若不存在,说明理由.
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com