
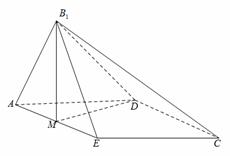
如图,已知等腰梯形 中,
中,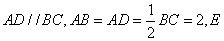 是
是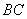 的中点,
的中点,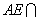
 ,将
,将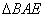 沿着
沿着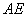 翻折成
翻折成 ,使平面
,使平面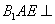 平面
平面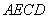 .
.
(I) 求证: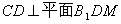 ;
;
(II)求二面角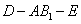 的余弦值;
的余弦值;
(III)在线段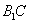 上是否存在点P,使得
上是否存在点P,使得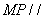 平面
平面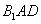 ,若存在,求出
,若存在,求出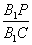 的值;若不存在,说明理由.
的值;若不存在,说明理由.
|
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
在篮球比赛中,某篮球队队员投进三分球的个数如表所示:
| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数 |
|
|
|
|
|
|
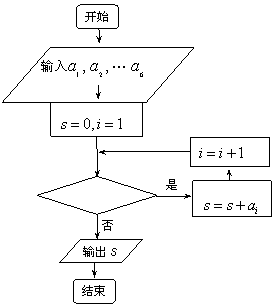
右图是统计上述6名队员在比赛中投进的三分球总数s的程序框图,则图中的判断框内应填入的条件是
A. 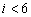 B.
B.  C.
C. 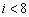 D.
D. 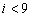
查看答案和解析>>
科目:高中数学 来源: 题型:
点P在平面上做匀速直线运动,速度向量v=(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为|v|个单位).设开始时点P的坐标为(-10,10),则5秒后质点P的坐标为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com