
【题目】已知椭圆![]() .
.
(1)若椭圆的离心率为![]() ,且点
,且点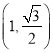 在椭圆上,①求椭圆的方程;
在椭圆上,①求椭圆的方程;
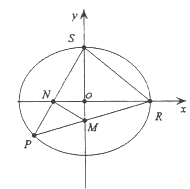
②设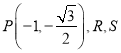 分别为椭圆
分别为椭圆![]() 的右顶点和上顶点,直线
的右顶点和上顶点,直线![]() 和
和![]() 与
与![]() 轴和
轴和![]() 轴相交于点
轴相交于点![]() ,求直线
,求直线![]() 的方程;
的方程;
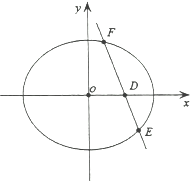
(2)设 ![]() 过
过![]() 点的直线
点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 均在
均在![]() 的右侧,
的右侧, ![]() ,求椭圆离心率的取值范围.
,求椭圆离心率的取值范围.
科目:高中数学 来源: 题型:
【题目】已知复数z的实部和虚部都是整数,
(1)若复数z为纯虚数,且|z﹣1|=|﹣1+i|,求复数z;
(2)若复数z满足z+ ![]() 是实数,且1<z+
是实数,且1<z+ ![]() ≤6,求复数z.
≤6,求复数z.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2007年到2011年人口总数与年份的关系如表所示
年份2007+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据表提供的数据,求最小二乘法求出y关于x的线性回归方程;
(2)据此估计2012年该城市人口总数.
参考公式: 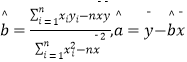 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在近30天内每件的销售价格P(元)与时间t(天)的函数关系是P= ![]() ,该商场的日销售量Q=﹣t+40(0<t≤30,t∈N),求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天.
,该商场的日销售量Q=﹣t+40(0<t≤30,t∈N),求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com