
【题目】已知函数![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)若不等式![]() 在区间
在区间![]() 上恒成立,求
上恒成立,求![]() 的取值范围,并证明:
的取值范围,并证明:
![]() .
.
【答案】(1)![]() 时,
时,![]() 在
在![]() 上递减,
上递减,![]() 时,
时,![]() 时递减,
时递减,![]() 时递增;(2)证明见解析.
时递增;(2)证明见解析.
【解析】试题分析:(1)判断单调性,定义域为![]() ,只要求得导数
,只要求得导数![]() ,判断
,判断![]() 的正负即可,此题需要按
的正负即可,此题需要按![]()
![]() 和
和![]() 分类讨论;(2)证明此不等式的关键是求
分类讨论;(2)证明此不等式的关键是求![]() 的最大值,由导数的知识可得
的最大值,由导数的知识可得![]() 最大值为
最大值为![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() .这样要证不等式的左边每一项都有
.这样要证不等式的左边每一项都有![]() ,相加即得结论.
,相加即得结论.
试题解析:(1)由题可知![]() ,
,
定义域为![]() ,
,
所以![]() ,
,
若![]() ,
,![]() 恒成立,
恒成立,![]() 在
在![]() 单调递减.
单调递减.
若![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
(2)不等式![]() 在区间
在区间![]() 上恒成立
上恒成立
可转化为:![]() ,令
,令![]() ,
,
则问题可化为![]() (其中
(其中![]() ),
),
由于![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() ,因此
,因此![]() , 即
, 即![]() .
.
由![]() ,可知
,可知![]() ,
,
从而得到![]() ,对
,对![]() 依次取值
依次取值![]() 可得
可得
![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,
对上述不等式两边依次相加得到:
![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系![]() 中,已知曲线
中,已知曲线![]() :
: ![]() ,
, ![]() :
: ![]() ,
, ![]() :
: ![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() .
.
(1)求点![]() 的极坐标;
的极坐标;
(2)若直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于两不同的点
交于两不同的点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() .
.
(1)若椭圆的离心率为![]() ,且点
,且点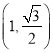 在椭圆上,①求椭圆的方程;
在椭圆上,①求椭圆的方程;
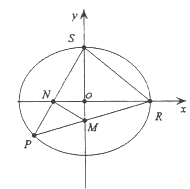
②设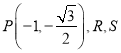 分别为椭圆
分别为椭圆![]() 的右顶点和上顶点,直线
的右顶点和上顶点,直线![]() 和
和![]() 与
与![]() 轴和
轴和![]() 轴相交于点
轴相交于点![]() ,求直线
,求直线![]() 的方程;
的方程;
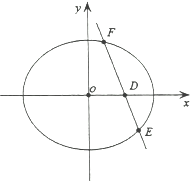
(2)设 ![]() 过
过![]() 点的直线
点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 均在
均在![]() 的右侧,
的右侧, ![]() ,求椭圆离心率的取值范围.
,求椭圆离心率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有( )
①用反证法证明命题“a,b∈R,方程x3+ax+b=0至少有一个实根”时,要作的假设是“方程至多有两个实根”;
②用数学归纳法证明“1+2+22+…+2n+2=2n+3﹣1,在验证n=1时,左边的式子是1+2+22;
③用数学归纳法证明 ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() (n∈N*)的过程中,由n=k推导到n=k+1时,左边增加的项为
(n∈N*)的过程中,由n=k推导到n=k+1时,左边增加的项为 ![]() +
+ ![]() ,没有减少的项;
,没有减少的项;
④演绎推理的结论一定正确;
⑤要证明“ ![]() ﹣
﹣ ![]() >
> ![]() ﹣
﹣ ![]() ”的最合理的方法是分析法.
”的最合理的方法是分析法.
A.①④
B.④
C.②③⑤
D.⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三化学得分训练的学生中随机抽出60名学生,将其化学成绩(均为整数)分成六段![]() 、
、![]() 、…、
、…、![]() 后得到部分频率分布直方图(如图).
后得到部分频率分布直方图(如图).
观察图形中的信息,回答下列问题:
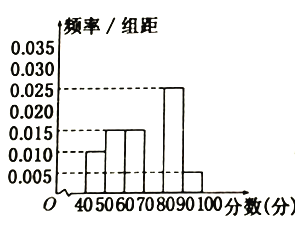
(1)求分数在![]() 内的频率,并补全频率分布直方图;
内的频率,并补全频率分布直方图;
(2)据此估计本次考试的平均分;
(3)若从60名学生中随机抽取2人,抽到的学生成绩在![]() 内记0分,在
内记0分,在![]() 内记1分,在
内记1分,在![]() 内记2分,用
内记2分,用![]() 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两地相距12km.A车、B车先后从甲地出发匀速驶向乙地.A车从甲地到乙地需行驶15min;B车从甲地到乙地需行驶10min.若B车比A车晚出发2min:
(1)分别写出A,B两车所行路程关于A车行驶时间的函数关系式;
(2)A,B两车何时在途中相遇?相遇时距甲地多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在双曲线 ![]() 中,F1 , F2分别是左右焦点,A1 , A2 , B1 , B2分别为双曲线的实轴与虚轴端点,若以A1A2为直径的圆总在菱形F1B1F2B2的内部,则此双曲线
中,F1 , F2分别是左右焦点,A1 , A2 , B1 , B2分别为双曲线的实轴与虚轴端点,若以A1A2为直径的圆总在菱形F1B1F2B2的内部,则此双曲线 ![]() 离心率的取值范围是( )
离心率的取值范围是( )
A.![]()
B.[ ![]() ,+∞)
,+∞)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各小题中,P是q的充要条件的是(08年山东理改编)
1)p:m<﹣2或m>6;q:y=x2+mx+m+3有两个不同的零点.
2)p: ![]() =1,q:y=f(x)是偶函数.
=1,q:y=f(x)是偶函数.
3)p:cosα=cosβ,q:tanα=tanβ.
4)p:A∩B=A,q:CUBCUA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() (a>0,b>0).
(a>0,b>0).
(1)当a=b=1时,证明:f(x)不是奇函数;
(2)设f(x)是奇函数,求a与b的值;
(3)在(2)的条件下,试证明函数f(x)的单调性,并解不等式f(1﹣m)+f(1+m2)<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com