
【题目】一副扑克牌有52张(不包括大小王),求:
(1)任取1张是红桃的概率;
(2)任取2张是同花色的概率;
(3)任取3张,至少有2张是同花色的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用古典概率求解,明确总数和红桃的张数即可;
(2)利用古典概率求解,求出总的基本事件共有![]() 种,同花色的共有
种,同花色的共有![]() 种,然后可得概率;
种,然后可得概率;
(3)利用古典概率求解,求出总的基本事件共有![]() 种,求出“至少有2张是同花色”包含的基本事件数,然后可得概率,也可以利用对立事件求解概率.
种,求出“至少有2张是同花色”包含的基本事件数,然后可得概率,也可以利用对立事件求解概率.
(1)52张牌中任取1张共有52种等可能结果,而取出是红桃的有13种,所以概率为![]() .
.
(2)52张牌中任取2张共有![]() 种等可能结果,而取出是同花色的共有
种等可能结果,而取出是同花色的共有![]() 种,所以概率为
种,所以概率为![]() .
.
(3)解法1 52张牌中任取3张共有![]() 种等可能结果,至少有2张同花色的共有
种等可能结果,至少有2张同花色的共有![]() 种,
种,
所以概率为![]() .
.
解法2 “任取3张,至少有2张是同花色”的对立事件是“任取3张是互不相同的花色”,
所以概率为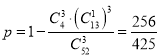 .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线
轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)将曲线![]() 的极坐标方程化为直角坐标方程,写出直线
的极坐标方程化为直角坐标方程,写出直线![]() 的参数方程的标准形式;
的参数方程的标准形式;
(2)已知直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为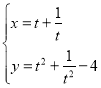 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,(
,(![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求线段
两点,求线段![]() 的长度
的长度![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,底面△
中,底面△![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
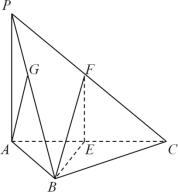
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得三棱锥
,使得三棱锥![]() 体积为
体积为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】家具公司制作木质的书桌和椅子,需要木工和漆工两道工序,已知木工平均四个小时做一把椅子,八个小时做一张书桌,该公司每星期木工最多有8000个工作时;漆工平均两小时漆一把椅子、一小时漆一张书桌,该公司每星期漆工最多有1300个工作时,又已知制作一把椅子和一张书桌的利润分别是15元和20元,试根据以上条件,问怎样安排生产能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形图表示学生人数依次记为A1、A2、…A10(如A2表示身高(单位:cm)在[150,155![]() 内的人数].图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是
内的人数].图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是


A.i<6B.i<7C.i<8D.i<9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对有![]() 个元素的总体
个元素的总体![]() 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体![]() 和
和![]() (m是给定的正整数,且
(m是给定的正整数,且![]() ),再从每个子总体中各随机抽取2个元素组成样本,用
),再从每个子总体中各随机抽取2个元素组成样本,用![]() 表示元素i和j同时出现在样本中的概率,则
表示元素i和j同时出现在样本中的概率,则![]() _________;所有
_________;所有![]() 的和等于________.
的和等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com