
分析 法1:可画出图形,可以得出$\overrightarrow{AC}=-(\overrightarrow{CB}+\overrightarrow{CD})$,$\overrightarrow{BE}=-\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CD}$,然后进行数量积的运算即可求出$\overrightarrow{AC}•\overrightarrow{BE}$的值.
法2:建立直角坐标系,利用向量法解决.
解答 解:如图,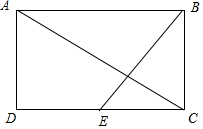
$\overrightarrow{AC}=-(\overrightarrow{CB}+\overrightarrow{CD})$,$\overrightarrow{BE}=\overrightarrow{BC}+\overrightarrow{CE}=-\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CD}$;
∴$\overrightarrow{AC}•\overrightarrow{BE}=-(\overrightarrow{CB}+\overrightarrow{CD})•(-\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CD})$
=${\overrightarrow{CB}}^{2}+\frac{1}{2}\overrightarrow{CB}•\overrightarrow{CD}-\frac{1}{2}{\overrightarrow{CD}}^{2}$
=1+0-2
=-1.
法2:分别以DC,DA所在直线为x,y轴,建立如图所示平面直角坐标系,则: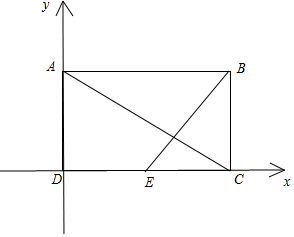
A(0,1),C(2,0),B(2,1),E(1,0);
∴$\overrightarrow{AC}=(2,-1),\overrightarrow{BE}=(-1,-1)$;
∴$\overrightarrow{AC}•\overrightarrow{BE}=-2+1=-1$;
故答案为:-1.
点评 考查向量加法的平行四边形法则,相反向量的概念,向量数乘的几何意义,以及数量积的运算,向量垂直的充要条件.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:选择题
| A. | x<-1 | B. | x>-1 | C. | x≤-1 | D. | x≥-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1009 | B. | 1008 | C. | 1007 | D. | 1006 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,点P是?ABCD边AB上的一点,射线CP交DA的延长线于点E,若$\frac{AP}{CD}$=$\frac{2}{5}$,则$\frac{{S}_{△AEP}}{{S}_{△BCP}}$=$\frac{4}{9}$.
如图,点P是?ABCD边AB上的一点,射线CP交DA的延长线于点E,若$\frac{AP}{CD}$=$\frac{2}{5}$,则$\frac{{S}_{△AEP}}{{S}_{△BCP}}$=$\frac{4}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com