
(本小题满分13分)已知数列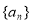 ,
, 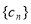 满足条件:
满足条件:
 ,
, 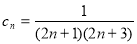 .
.
(Ⅰ)求证数列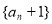 是等比数列,并求数列
是等比数列,并求数列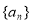 的通项公式;
的通项公式;
(Ⅱ)求数列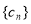 的前
的前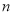 项和
项和 ,并求使得
,并求使得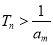 对任意
对任意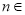
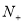 都成立的正整数
都成立的正整数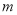 的最小值.
的最小值.
(Ⅰ)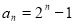 ;(Ⅱ)5
;(Ⅱ)5
【解析】
试题分析:(Ⅰ)由数列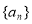 满足
满足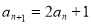 ,通过构造即可得到数列
,通过构造即可得到数列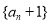 为等比数列,并求出数列
为等比数列,并求出数列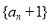 的通项,由此得到数列
的通项,由此得到数列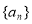 的通项公式.
的通项公式.
(Ⅱ)由数列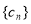 满足
满足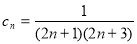 .由裂项求和法即可得到数列
.由裂项求和法即可得到数列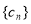 的前
的前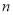 项和
项和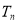 .又由
.又由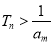 对任意
对任意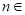
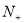 都成立,所以要求出
都成立,所以要求出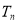 的最小值,通过对数列通项的研究即可得数列
的最小值,通过对数列通项的研究即可得数列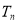 是一个递增的数列,由此可得
是一个递增的数列,由此可得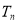 的最小值为
的最小值为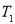 .再根据
.再根据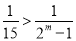 即可求出结论.
即可求出结论.
试题解析:(Ⅰ)∵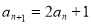
∴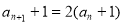 ,∵
,∵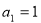 ,
,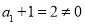 2分
2分
∴数列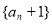 是首项为2,公比为2的等比数列 .
是首项为2,公比为2的等比数列 .
∴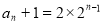 ∴
∴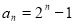 5分
5分
(Ⅱ)∵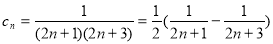 , 7分
, 7分
∴
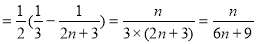 . 9分
. 9分
∵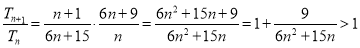 ,又
,又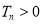 ,
,
∴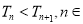 N*,即数列
N*,即数列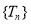 是递增数列.
是递增数列.
∴当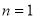 时,
时,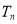 取得最小值
取得最小值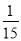 . 11分
. 11分
要使得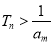 对任意
对任意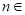 N*都成立,结合(Ⅰ)的结果,只需
N*都成立,结合(Ⅰ)的结果,只需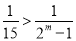 ,由此得
,由此得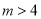 .∴正整数
.∴正整数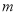 的最小值是5. 13分
的最小值是5. 13分
考点:1.等比数列的性质.2.裂项法求和.3.数列与不等式的关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年安徽省江淮名校高三第二次联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)利用已学知识证明:
(1)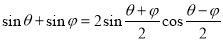 。
。
(2)已知△ABC的外接圆的半径为2,内角A,B,C满足 ,求△ABC的面积。
,求△ABC的面积。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省文登市高三上学期第一次考试理科数学试卷(解析版) 题型:选择题
将函数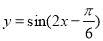 图象向左平移
图象向左平移 个单位,所得函数图象的一条对称轴的方程是( )
个单位,所得函数图象的一条对称轴的方程是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省济宁市高三上学期期中考试文科数学试卷(解析版) 题型:填空题
给出下列四个命题:
①若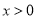 ,且
,且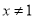 则
则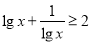 ;
;
②设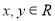 ,命题“若
,命题“若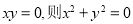 ”的否命题是真命题;
”的否命题是真命题;
③函数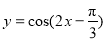 的一条对称轴是直线
的一条对称轴是直线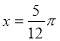 ;
;
④若定义在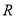 上的函数
上的函数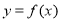 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意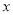 必有
必有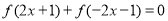 .
.
其中,所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省襄阳市高三上学期11月质检文科数学试卷(解析版) 题型:填空题
已知直线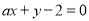 与圆心为
与圆心为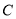 的圆
的圆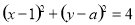 相交于
相交于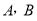 两点,且
两点,且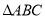 为直角三角形,则实数
为直角三角形,则实数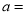 _________.
_________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省临沂市四校联考高一上学期期中考试数学试卷(解析版) 题型:填空题
给出下列命题:①函数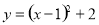 在
在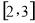 上的值域为
上的值域为 ;②函数
;②函数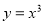 ,
,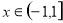 是奇函数;③函数
是奇函数;③函数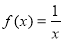 在
在 上是减函数;其中正确命题的个数有 .(将正确的序号都填上)
上是减函数;其中正确命题的个数有 .(将正确的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com