Question

已知数列{a_n}的前n项和为S_n，S_n=2a_n-n（n∈N^*）则=________．

Answer 1

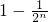
分析：先根据条件求出a₁=1；再根据S_n=2a_n-n得到S_n+1=2a_n+1-（n+1）；两式作差可得a_n+1-a_n=a_n+1以及a_n+1=2a_n+1，进而推出数列{a_n+1}是以a₁+1=2为首项，2为公比的等比数列；再代入所求即可得到结论．
解答：由题得：S₁=2a₁-1?a₁=1．
∵S_n=2a_n-n ①，
∴S_n+1=2a_n+1-（n+1）②
②-①得：a_n+1=2a_n+1-2a_n-1
所以有：a_n+1-a_n=a_n+1 ③
以及a_n+1=2a_n+1?a_n+1+1=2（a_n+1）?数列{a_n+1}是以a₁+1=2为首项，2为公比的等比数列．
∴a_n+1=（a₁+1）q^n-1=2×2^n-1=2ⁿ．
∴
=
=
=
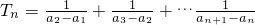
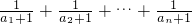
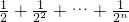
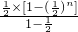
=1-．
故答案为：1-．
点评：本题主要考查了利用数列的递推公式求数列的和．是一道很好的题目，解决问题的关键在于利用S_n=2a_n-n得到S_n+1=2a_n+1-（n+1）；两式作差可得a_n+1-a_n=a_n+1以及a_n+1=2a_n+1，进而推出数列{a_n+1}是以a₁+1=2为首项，2为公比的等比数列．
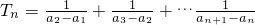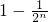
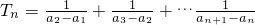
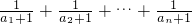
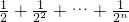
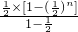