
在等差数列{an}和等比数列{bn}中,a1=1,b1=2,bn>0(n∈N*),且b1,a2,b2成等差数列,a2,b2,a3+2成等比数列,数列{bn}的前n项和为Sn.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)若Sn+an>m对任意的正整数n恒成立,求常数m的取值范围.
(Ⅰ)an=3n﹣2,bn=2•3n﹣1;(Ⅱ){m|m<3}
【解析】
试题分析:(Ⅰ)设等差数列{an}的公差为d,等比数列{bn}的公比为q(q>0),由已知得 ,解得d=q=3,所以an=3n﹣2,bn=2•3n﹣1;(Ⅱ)由(Ⅰ)知
,解得d=q=3,所以an=3n﹣2,bn=2•3n﹣1;(Ⅱ)由(Ⅰ)知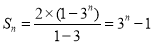 ,从而
,从而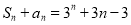 ,则3n+3n﹣3>m对任意的正整数n恒成立,构造函数f(n)=3n+3n﹣3,则
,则3n+3n﹣3>m对任意的正整数n恒成立,构造函数f(n)=3n+3n﹣3,则
f(n+1)﹣f(n)=2•3n﹣3>0即f(n)单调递增,所以m<f(1)=3,答案为{m|m<3}.
试题解析:(Ⅰ)设等差数列{an}的公差为d,等比数列{bn}的公比为q(q>0).
由题意,得 ,解得d=q=3.
,解得d=q=3.
∴an=3n﹣2,bn=2•3n﹣1;
(Ⅱ)∵Sn+an>m对任意的正整数n恒成立,
∴3n+3n﹣3>m对任意的正整数n恒成立,
令f(n)=3n+3n﹣3,则f(n+1)﹣f(n)=2•3n﹣3>0,
∴f(n)单调递增,
∴m<f(1)=3.
∴常数m的取值范围{m|m<3}
考点:1.等差数列和等比数列的通项公式;2.等比数列的求和公式;3.与正整数有关的不等式恒成立问题


科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试理科数学试卷(解析版) 题型:选择题
若函数y=loga(x2﹣ax+1)有最小值,则a的取值范围是( )
A.0<a<1 B.0<a<2,a≠1 C.1<a<2 D.a≥2
查看答案和解析>>
科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试理科数学试卷(解析版) 题型:选择题
若集合A={x|﹣2<x<1},B={x|0<x<2},则集合A∩B=( )
A.{x|﹣1<x<1} B.{x|﹣2<x<1}
C.{x|﹣2<x<2} D.{x|0<x<1}
查看答案和解析>>
科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试文科数学试卷(解析版) 题型:填空题
设公比为q(q>0)的等比数列{an}的前n项和为Sn.若S2=3a2+2,S4=3a4+2,则q= _________ .
查看答案和解析>>
科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试文科数学试卷(解析版) 题型:选择题
已知两条不同的直线m、n,两个不同的平面a、β,则下列命题中的真命题是( )
A.若m⊥a,n⊥β,a⊥β,则m⊥n B.若m⊥a,n∥β,a⊥β,则m⊥n
C.若m∥a,n∥β,a∥β,则m∥n D.若m∥a,n⊥β,a⊥β,则m∥n
查看答案和解析>>
科目:高中数学 来源:2015届浙江省绍兴市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
球O为边长为2的正方体ABCD-A1B1C1D1的内切球,P为球O的球面上动点,M为B1C1中点,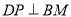 ,则点P的轨迹周长为( ).
,则点P的轨迹周长为( ).
A . B.
B.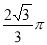 C.
C. D.
D.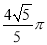
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com