
分析 (Ⅰ)当ω=1时,利用两角和与差以及二倍角公式化简函数的解析式,然后求解函数的单调区间.
(Ⅱ)化简函数的解析式为:f(x)=$sin(ωx+\frac{π}{3})$.通过$f(\frac{π}{3})=1$,求出$ω=6n+\frac{1}{2}$.然后求解T的最大值.
解答 (本小题满分13分)
解:(Ⅰ)当ω=1时,$f(x)=\frac{1}{2}sinx+\sqrt{3}{cos^2}\frac{x}{2}-\frac{{\sqrt{3}}}{2}$=$\frac{1}{2}sinx+\frac{{\sqrt{3}}}{2}cosx$=$sin(x+\frac{π}{3})$.
令$2kπ-\frac{π}{2}≤x+\frac{π}{3}≤2kπ+\frac{π}{2}{,^{\;}}k∈Z$.
解得$2kπ-\frac{5π}{6}≤x≤2kπ+\frac{π}{6}{,^{\;}}k∈Z$.
所以f(x)的单调递增区间是$[2kπ-\frac{5π}{6},2kπ+\frac{π}{6}],k∈Z$.…(7分)
(Ⅱ)由$f(x)=\frac{1}{2}sinωx+\sqrt{3}{cos^2}\frac{ωx}{2}-\frac{{\sqrt{3}}}{2}$=$\frac{1}{2}sinωx+\frac{{\sqrt{3}}}{2}cosωx$=$sin(ωx+\frac{π}{3})$.
因为$f(\frac{π}{3})=1$,所以$sin(\frac{πω}{3}+\frac{π}{3})=1$.
则$\frac{πω}{3}+\frac{π}{3}=2nπ+\frac{π}{2}$,n∈Z.
解得$ω=6n+\frac{1}{2}$.
又因为函数f(x)的最小正周期$T=\frac{2π}{ω}$,且ω>0,
所以当ω=$\frac{1}{2}$时,T的最大值为4π. …(13分)
点评 本题考查三角函数的化简求值,二倍角公式以及两角和与差的三角函数的应用,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A、B是水平面上两个点,相距800m,在A点测得山顶C的仰角是25°,∠BAD=40°,又在点B测得∠ABD=40°,其中D点是点C在水平面上的垂足.求山高CD(精确到1m).
如图,A、B是水平面上两个点,相距800m,在A点测得山顶C的仰角是25°,∠BAD=40°,又在点B测得∠ABD=40°,其中D点是点C在水平面上的垂足.求山高CD(精确到1m).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
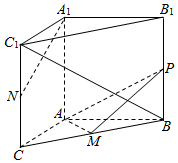 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪N | B. | M∩N | C. | (∁UM)∪(∁UN) | D. | (∁UM)∩(∁UN) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{3}$+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com