
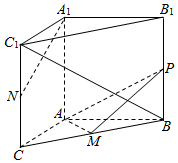
 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.分析 (Ⅰ)由已知推导出AM⊥BC,BB1⊥底面ABC,BB1⊥AM,从而AM⊥平面BB1C1C,由此能证明平面APM⊥平面BB1C1C.
(Ⅱ)取C1B1中点D,连结A1D,DN,DM,B1C,则四边形A1AMD为平行四边形,从而A1D∥AM,进而A1D∥平面APM;进一步推导出DN∥B1C,MP∥B1C,则DN∥MP,从而DN∥平面APM,进而平面A1DN∥平面APM,由此能证明A1N∥平面APM.
(Ⅲ)假设BC1与平面APM垂直,则BC1⊥PM.设PB=x,$x∈[0,\sqrt{3}]$.推导出$x=\frac{{4\sqrt{3}}}{3}∉[0,\sqrt{3}]$,从而得到直线BC1与平面APM不能垂直.
解答 (本小题满分14分)
证明:(Ⅰ)由已知,M为BC中点,且AB=AC,所以AM⊥BC.
又因为BB1∥AA1,且AA1⊥底面ABC,所以BB1⊥底面ABC.
因为AM?底面ABC,所以BB1⊥AM,
又BB1∩BC=B,
所以AM⊥平面BB1C1C.
又因为AM?平面APM,
所以平面APM⊥平面BB1C1C. …(5分)
(Ⅱ)取C1B1中点D,连结A1D,DN,DM,B1C.
由于D,M分别为C1B1,CB的中点,所以DM∥A1A,且DM=A1A.
则四边形A1AMD为平行四边形,所以A1D∥AM.
又A1D?平面APM,AM?平面APM,所以A1D∥平面APM.
由于D,N分别为C1B1,C1C的中点,所以DN∥B1C.
又P,M分别为B1B,CB的中点,所以MP∥B1C.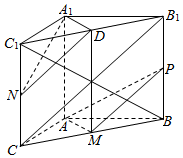
则DN∥MP.又DN?平面APM,MP?平面APM,所以DN∥平面APM.
由于A1D∩DN=D,所以平面A1DN∥平面APM.
由于A1N?平面A1DN,所以A1N∥平面APM.…10分
解:(Ⅲ)假设BC1与平面APM垂直,
由PM?平面APM,则BC1⊥PM.
设PB=x,$x∈[0,\sqrt{3}]$.当BC1⊥PM时,∠BPM=∠B1C1B,
所以$\user2{Rt}△PBM$∽Rt△∠B1C1B,所以$\frac{PB}{MB}=\frac{{{C_1}{B_1}}}{{B{B_1}}}$.
由已知$MB=\sqrt{2},{C_1}{B_1}=2\sqrt{2},B{B_1}=\sqrt{3}$,
所以$\frac{x}{{\sqrt{2}}}=\frac{{2\sqrt{2}}}{{\sqrt{3}}}$,得$x=\frac{{4\sqrt{3}}}{3}$.
由于$x=\frac{{4\sqrt{3}}}{3}∉[0,\sqrt{3}]$,
因此直线BC1与平面APM不能垂直. …(14分)
点评 本题考查面面垂直的证明,考查线面平行的证明,考查线面是否存在的判断与证明,是中档题,解题时要认真审题,注意空间思维能力的培养.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源: 题型:填空题
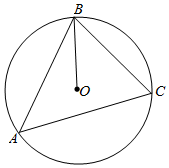 如图所示,圆O是△ABC的外接圆,BA=m,BC=$\frac{4}{m}$,∠ABC=60°,若$\overrightarrow{BO}=x\overrightarrow{BA}$+y$\overrightarrow{BC}$,则x+y的最大值是$\frac{2}{3}$.
如图所示,圆O是△ABC的外接圆,BA=m,BC=$\frac{4}{m}$,∠ABC=60°,若$\overrightarrow{BO}=x\overrightarrow{BA}$+y$\overrightarrow{BC}$,则x+y的最大值是$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$经过点 $(\frac{6}{5},\frac{4}{5})$,其离心率为$\frac{{\sqrt{3}}}{2}$,设A,B,M是椭圆C上的三点,且满足 $\overrightarrow{OM}=cosα•\overrightarrow{OA}+sinα•\overrightarrow{OB}$$(α∈(0,\frac{π}{2}))$,其
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$经过点 $(\frac{6}{5},\frac{4}{5})$,其离心率为$\frac{{\sqrt{3}}}{2}$,设A,B,M是椭圆C上的三点,且满足 $\overrightarrow{OM}=cosα•\overrightarrow{OA}+sinα•\overrightarrow{OB}$$(α∈(0,\frac{π}{2}))$,其查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com