
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
分析 根据题意,分析“凹数”的定义,根据十位数分类讨论即可求出凹数的个数,再利用古典概型概率计算公式即可得到所求概率.
解答 解:根据题意,当且仅当a>b且c>b时称为“凹数”,
在{4,5,6,7,8}的5个整数中任取3个不同的数组成三位数,有A53=60种取法,
在{4,5,6,7,8}的5个整数中任取3个不同的数,将4放在十位上,再排2个数排在百、个位上,有A42=12种情况,
将5放在十位上,再排2个数排在百、个位上,有A32=6种情况,
将6放在十位上,再排2个数排在百、个位上,有A22=2种情况,
根据分类计数原理可得12+6+2=20种,
故它为“凹数”的概率是$\frac{20}{60}$=$\frac{1}{3}$.
故选:C.
点评 本题考查组合数公式的运用,关键在于根据题干中所给的“凹数”的定义,再利用古典概型概率计算公式即得答案.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A、B是水平面上两个点,相距800m,在A点测得山顶C的仰角是25°,∠BAD=40°,又在点B测得∠ABD=40°,其中D点是点C在水平面上的垂足.求山高CD(精确到1m).
如图,A、B是水平面上两个点,相距800m,在A点测得山顶C的仰角是25°,∠BAD=40°,又在点B测得∠ABD=40°,其中D点是点C在水平面上的垂足.求山高CD(精确到1m).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
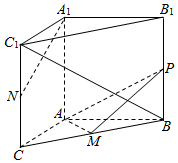 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪N | B. | M∩N | C. | (∁UM)∪(∁UN) | D. | (∁UM)∩(∁UN) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com