
分析 (1)将椭圆方程化为标准方程,由题意可得a,可得b,即可得到椭圆方程,再由离心率公式计算即可得到所求值;
(2)设AP中点为D,由|BA|=||BP|,所以BD⊥AP,求得AP的斜率,进而得到BD的斜率和中点,可得直线BD的方程,即有B的坐标,求得四边形OPAB的面积为S=S△OAP+S△OMB,化简整理,运用基本不等式即可得到最小值.
解答 解:(1)椭圆C:mx2+3my2=1,即为$\frac{{x}^{2}}{\frac{1}{m}}$+$\frac{{y}^{2}}{\frac{1}{3m}}$=1,所以a2=$\frac{1}{m}$,b2=$\frac{1}{3m}$,
a2=$\frac{1}{m}$,b2=$\frac{1}{3m}$,可得2a=2$\frac{1}{\sqrt{m}}$=2$\sqrt{6}$,
m=$\frac{1}{6}$,可得a=$\sqrt{6}$,b=$\sqrt{2}$,
即有椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,
由c=$\sqrt{{a}^{2}-{b}^{2}}$=2,即e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$;
(2)设AP中点为D,由|BA|=||BP|,所以BD⊥AP,
由题意,可得直线BD的斜率存在,P(x0,y0)(y0≠0),
则D($\frac{{x}_{0}+3}{2}$,$\frac{{y}_{0}}{2}$),直线AP的斜率为kAP=$\frac{{y}_{0}}{{x}_{0}-3}$,
直线BD的斜率为-$\frac{1}{{k}_{AP}}$=$\frac{3-{x}_{0}}{{y}_{0}}$,
可得BD的方程为y-$\frac{{y}_{0}}{2}$=$\frac{3-{x}_{0}}{{y}_{0}}$(x-$\frac{{x}_{0}+3}{2}$),
令x=0可得y=$\frac{{{x}_{0}}^{2}+{{y}_{0}}^{2}-9}{2{y}_{0}}$,即B(0,$\frac{{{x}_{0}}^{2}+{{y}_{0}}^{2}-9}{2{y}_{0}}$),
由$\frac{{{x}_{0}}^{2}}{6}$+$\frac{{{y}_{0}}^{2}}{2}$=1,可得x02=6-3y02,
化简可得B(0,$\frac{-2{{y}_{0}}^{2}-3}{2{y}_{0}}$),
则四边形OPAB的面积为S=S△OAP+S△OMB=$\frac{1}{2}$×3|y0|+$\frac{1}{2}$×3|$\frac{-2{{y}_{0}}^{2}-3}{2{y}_{0}}$|
=$\frac{3}{2}$(2|y0|+$\frac{3}{2|{y}_{0}|}$)≥$\frac{3}{2}$•2$\sqrt{2|{y}_{0}|•\frac{3}{2|{y}_{0}|}}$=3$\sqrt{3}$,
当且仅当2|y0|=$\frac{3}{2|{y}_{0}|}$,即y0=±$\frac{\sqrt{3}}{2}$∈[-$\sqrt{2}$,$\sqrt{2}$]时,等号成立.
所以四边形OPAB面积的最小值为3$\sqrt{3}$.
点评 本题考查椭圆的方程和离心率的求法,注意运用椭圆的性质和离心率公式,考查四边形面积的最值的求法,注意运用直线的斜率公式和基本不等式,考查化简整理的运算能力,属于中档题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:选择题
| A. | f(1)<f(-1)<f(0) | B. | f(0)<f(1)<f(-1) | C. | f(-1)<f(0)<f(1) | D. | f(1)<f(0)<f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
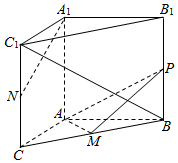 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪N | B. | M∩N | C. | (∁UM)∪(∁UN) | D. | (∁UM)∩(∁UN) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<3} | B. | {x|-1<x<0} | C. | {x|-2<x<0} | D. | {x|-3<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com