
【题目】![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,求证:
,求证:![]() .
.
【答案】(1)详见解析(2)详见解析
【解析】
试题分析:(1)先求函数导数![]()
![]() ,再根据定义域研究导函数零点:当
,再根据定义域研究导函数零点:当![]() 时,仅有一个零点;当
时,仅有一个零点;当![]() 时,有两个零点;列表分析导函数符号变号规律得单调区间(2)根据(1)得
时,有两个零点;列表分析导函数符号变号规律得单调区间(2)根据(1)得![]() ,将不等式转化为证明
,将不等式转化为证明![]() ,构造函数
,构造函数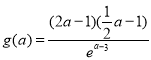 。利用导数可得
。利用导数可得
试题解析:(1)![]() ,
,![]() ,
,
则![]()
![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调增,
上单调增,![]() 上单调减,
上单调减,
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,![]() ,
,
当![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]() 的解集为
的解集为![]() ,
,![]() ;
;![]() 的解集为
的解集为![]() ,
,
∴函数![]() 的单调递增区间为:
的单调递增区间为:![]() ,
,![]() ,
,
函数![]() 的单调递减区间为
的单调递减区间为![]() ;
;
当![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]() 的解集为
的解集为![]() ;
;![]() 的解集为
的解集为![]() ,
,
综上可知:![]() ,函数
,函数![]() 的单调递增区间为:
的单调递增区间为:![]() ,
,![]() ,函数
,函数![]() 的单调递减区间为
的单调递减区间为![]() ;
;![]() ,函数
,函数![]() 的单调递增区间为
的单调递增区间为![]() ,函数
,函数![]() 的单调递减区间为
的单调递减区间为![]() .
.
(2)证明:∵![]() ,故由(1)可知函数
,故由(1)可知函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
∴![]() 在
在![]() 时取极大值,并且也是最大值,即
时取极大值,并且也是最大值,即![]() ,
,
又∵![]()
![]() ,
,
∴![]() ,
,
设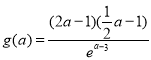 ,
,![]() ,
,
∴![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ,
,
∴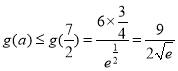 ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】小王于年初用50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小王在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售价格为(25-x)万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小王获得的年平均利润最大?(利润=累计收入+销售收入-总支出)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某隧道设计为双向四车道,车道总宽为![]() ,要求通行车辆限高
,要求通行车辆限高![]() ,隧道全长为
,隧道全长为![]() ,隧道的拱线可近似的看成半个椭圆形状.
,隧道的拱线可近似的看成半个椭圆形状.
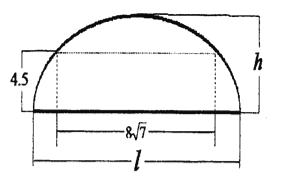
(1)若最大拱高![]() 为
为![]() ,则隧道设计的拱宽
,则隧道设计的拱宽![]() 是多少?
是多少?
(2)若最大拱高![]() 不小于
不小于![]() ,则应如何设计拱高
,则应如何设计拱高![]() 和拱宽
和拱宽![]() ,才能使隧道的土方工程量最小?
,才能使隧道的土方工程量最小?
(注: 1.半个椭圆的面积公式为![]() ;2.隧道的土方工程量=截面面积
;2.隧道的土方工程量=截面面积![]() 隧道长)
隧道长)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形的直棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵![]() 与刍童
与刍童![]() 的组合体中
的组合体中![]() ,
,![]() .台体体积公式:
.台体体积公式:![]() ,其中
,其中![]() 分别为台体上、下底面面积,
分别为台体上、下底面面积,![]() 为台体高.
为台体高.
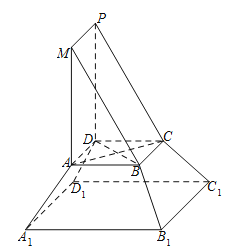
(Ⅰ)证明:直线![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,三棱锥
,三棱锥![]() 的体积
的体积![]() ,求该组合体的体积.
,求该组合体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,
,![]() ,且它的圆心在直线
,且它的圆心在直线![]() 上.
上.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)求圆![]() 关于直线
关于直线![]() 对称的圆的方程。
对称的圆的方程。
(Ⅲ)若点![]() 为圆
为圆![]() 上任意一点,且点
上任意一点,且点![]() ,求线段
,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() .设圆
.设圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上.
上.
(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com