
分析 (Ⅰ)求出函数的导数,得到f′(x)≤0恒成立,令$g(x)=lnx-\frac{1}{x}-2x+1+2a$,求出函数的导数,根据函数的单调性得到g(x)max≤0,求出a的范围即可;
(Ⅱ)根据f′(x1)=lnx1-$\frac{1}{{x}_{1}}$-2x1+1+2a①,f′(x2)=lnx2-$\frac{1}{{x}_{2}}$-2x2+1+2a②,得到:x1+x2的解析式,从而证明结论即可.
解答 解:(Ⅰ)由已知,$f'(x)=lnx+\frac{x-1}{x}-2(x-a)=lnx-\frac{1}{x}-2x+1+2a≤0$恒成立
令$g(x)=lnx-\frac{1}{x}-2x+1+2a$,则$g'(x)=\frac{1}{x}+\frac{1}{x^2}-2=\frac{{-2{x^2}+x+1}}{x^2}=\frac{-(2x+1)(x-1)}{x^2}(x>0)$,
-(2x+1)<0,令g′(x)>0,解得:0<x<1,令g′(x)<0,解得:x>1,
故g(x)在(0,1)递增,在(1,+∞)递减,
∴g(x)max=g(1)=2a-2∴由f'(x)≤0恒成立可得a≤1.
即当f(x)在(0,+∞)上单调递减时,a的取值范围是(-∞,1].
(Ⅱ)若f(x)有两个极值点x1,x2,不妨设0<x1<x2.
由(Ⅰ)可知a>1,且f′(x1)=lnx1-$\frac{1}{{x}_{1}}$-2x1+1+2a①,f′(x2)=lnx2-$\frac{1}{{x}_{2}}$-2x2+1+2a②,
由①-②得:$ln\frac{x_1}{x_2}+\frac{{{x_1}-{x_2}}}{{{x_1}{x_2}}}-2({x_1}-{x_2})=0$∴$({x_1}-{x_2})(\frac{1}{{{x_1}{x_2}}}-2)=-ln\frac{x_1}{x_2}>0$∴$\frac{1}{{{x_1}{x_2}}}<2$,即 ${x_1}{x_2}>\frac{1}{2}>\frac{1}{e}$,
由①+②得:$ln({x_1}{x_2})+2-\frac{{{x_1}+{x_2}}}{{{x_1}{x_2}}}-2({x_1}+{x_2})+4a=0$,
∴${x_1}+{x_2}=\frac{{ln({x_1}{x_2})+2+4a}}{{\frac{1}{{{x_1}{x_2}}}+2}}>\frac{-1+2+4}{2+2}=\frac{5}{4}$.
点评 本题考查导数的综合运用,考查学生应用知识解决问题的能力,较难题.


科目:高中数学 来源: 题型:选择题
| A. | [0,e2-e+1] | B. | [0,e2+e-1] | C. | [0,e2+e+1] | D. | [0,e2-e-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
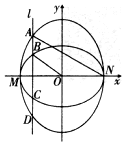 如图,已知椭圆C1的中心在原点O,长轴左、右端点M、N在x轴上,椭圆C2的短轴为MN,且C1、C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点纵坐标从大到小依次为A、B、C、D.
如图,已知椭圆C1的中心在原点O,长轴左、右端点M、N在x轴上,椭圆C2的短轴为MN,且C1、C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点纵坐标从大到小依次为A、B、C、D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
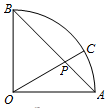 如图,扇形AOB的圆心角为90°,点P在弦AB上,且OP=$\sqrt{2}$AP,延长OP交弧AB于点C,现向该扇形内随机投一点,则该点落在扇形AOC内的概率为$\frac{1}{3}$.
如图,扇形AOB的圆心角为90°,点P在弦AB上,且OP=$\sqrt{2}$AP,延长OP交弧AB于点C,现向该扇形内随机投一点,则该点落在扇形AOC内的概率为$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
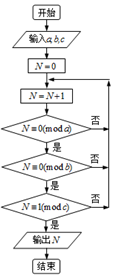 若正整数N除以正整数m后的余数为n,则记为N≡n(bmodm),例如10≡4(bmod6),如图程序框图的算法源于我国古代《孙子算经》中的“孙子定理”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )
若正整数N除以正整数m后的余数为n,则记为N≡n(bmodm),例如10≡4(bmod6),如图程序框图的算法源于我国古代《孙子算经》中的“孙子定理”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )| A. | 6 | B. | 9 | C. | 12 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 3 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com