练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知点在同一个球的上,,,.若四面体体积的最大值为,则这个球的表面积为（ ）

    A.B.C.D.

    【答案】B

    【解析】

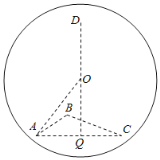
    根据几何体的特征,小圆的圆心为Q,若四面体ABCD的体积的最大值,由于底面积S△ABC不变,高最大时体积最大,可得DQ与面ABC垂直时体积最大,从而求出球的半径,即可求出球的表面积.

    根据题意知,A、B、C三点均在球心O的表面上,

    且,,,由余弦定理可得BC,

    ∴△ABC为直角三角形,

    ∴△ABC外接圆直径,即,

    且,

    的中点即为小圆的圆心设为Q,若四面体ABCD的体积的最大值,由于底面积S△ABC不变,高最大时体积最大,

    所以,DQ与面ABC垂直时体积最大,最大值为S△ABC×DQ,

    ∴,

    设球的半径为R,则

    在直角△AQO中,OA2＝AQ2+OQ2,即

    ∴,

    ∴球的表面积为,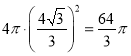

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若数列满足“对任意正整数，都存在正整数，使得”，则称数列具有“性质”.已知数列为无穷数列.

    （1）若为等比数列，且，判断数列是否具有“性质”，并说明理由；

    （2）若为等差数列，且公差，求证：数列不具有“性质”；

    （3）若等差数列具有“性质”，且，求数列的通项公式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为抛物线的焦点，为的准线与轴的交点，点在抛物线上，设，，，有以下个结论：

    ①的最大值是；②；③存在点，满足.

    其中正确结论的序号是______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，已知多面体的底面是边长为2的菱形，底面，且.

    （1）证明：平面；

    （2）若，求异面直线与所成角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】人口平均预期寿命是综合反映人们健康水平的基本指标.年第六次全国人口普查资料表明，随着我国社会经济的快速发展，人民生活水平的不断提高以及医疗卫生保障体系的逐步完善，我国人口平均预期寿命继续延长，国民整体健康水平有较大幅度的提高.下图体现了我国平均预期寿命变化情况，依据此图，下列结论错误的是（ ）

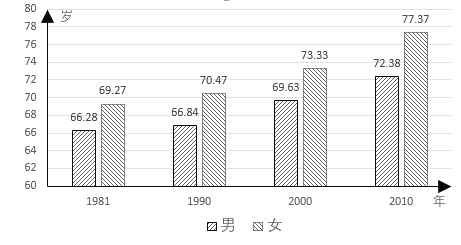
    A.男性的平均预期寿命逐渐延长

    B.女性的平均预期寿命逐渐延长

    C.男性的平均预期寿命延长幅度略高于女性

    D.女性的平均预期寿命延长幅度略高于男性

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为（为参数），直线的参数方程为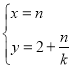（为参数）.设直线与的交点为，当变化时的点的轨迹为曲线.

    （1）求出曲线的普通方程；

    （2）以坐标原点为极点，轴正半轴为极轴建立极坐标系，设射线的极坐标方程为且，点是射线与曲线的交点，求点的极径.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四面体ABCD中，△ABC和△BCD均是边长为1的等边三角形，已知四面体ABCD的四个顶点都在同一球面上，且AD是该球的直径，则四面体ABCD的体积为( )

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝axex，g（x）＝x2+2x+b，若曲线y＝f（x）与曲线y＝g（x）都过点P（1，c）．且在点P处有相同的切线l．

    （Ⅰ）求切线l的方程；

    （Ⅱ）若关于x的不等式k[ef（x）]≥g（x）对任意x∈[﹣1，+∞）恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，点在轴上，点在轴上，且．当点在轴上运动时，点的轨迹记为曲．

    （Ⅰ）求曲线的轨迹方程；

    （Ⅱ）过曲线上一点，作圆的切线，交曲线于两点，若直线垂直于直线，求的面积．

    查看答案和解析>>

    同步练习册答案