
分析 (1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=2sin(2x+$\frac{π}{6}$),由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z可解得函数f(x)的单调递增区间,结合范围x∈[0,$\frac{π}{2}$],即可得解.
(2)由(1)可知:f(x)在[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递增,令t=f(x),则g(t)=-(1+λ)t2-2t+1在[-$\frac{π}{3}$,$\frac{π}{6}$]单调递减,根据二次函数的图象和性质分类讨论,从而解出实数λ的取值范围.
解答 解:(1)∵f(x)=(sinx+$\sqrt{3}$cox)2-2
=sin2x+3cos2x+2$\sqrt{3}$sinxcosx-2
=$\frac{1-cos2x}{2}$+3×$\frac{1+cos2x}{2}$+$\sqrt{3}$sin2x-2
=cos2x+$\sqrt{3}$sin2x
=2sin(2x+$\frac{π}{6}$),
∴由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z可解得函数f(x)的单调递增区间为:[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z,
∴当x∈[0,$\frac{π}{2}$]时,求函数f(x)的单调递增区间为:[0,$\frac{π}{6}$].
(2)由(1)可知:f(x)在[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递增,令t=f(x),则g(t)=-(1+λ)t2-2t+1在[-$\frac{π}{3}$,$\frac{π}{6}$]单调递减,
①当λ=-1时,g(t)=-2t+1满足;
②当-(1+λ)>0时,即λ<-1时,$\frac{-1}{1+λ}≥\frac{π}{6}$,可解得λ≥$-\frac{6}{π}-1$,
所以可得:-1>λ≥$-\frac{6}{π}-1$,
③当-(1+λ)<0时,即λ>-1时,$\frac{-1}{1+λ}$≤-$\frac{π}{3}$,解得λ≤-1+$\frac{3}{π}$,
所以可得:-1<λ≤-1+$\frac{3}{π}$,
综上可得:$-\frac{6}{π}-1$≤λ≤-1+$\frac{3}{π}$.
点评 本题主要考查了三角函数恒等变换的应用,考查了二次函数的图象和性质,考查了分类讨论思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)>e,f(2012)>e2012 | B. | f(1)>e,f(2012)<e2012 | ||
| C. | f(1)<e,f(2012)>e2012 | D. | f(1)<e,f(2012)<e2012 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
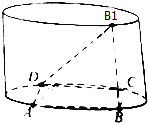 如图,圆柱底面直径为10,母线BB1=6,矩形ABCD内接于圆柱的下底面,BC=6,求直线DB1与BC所成角的大小.(结果用反三角函教值表示)
如图,圆柱底面直径为10,母线BB1=6,矩形ABCD内接于圆柱的下底面,BC=6,求直线DB1与BC所成角的大小.(结果用反三角函教值表示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com