
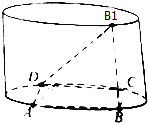
 如图,圆柱底面直径为10,母线BB1=6,矩形ABCD内接于圆柱的下底面,BC=6,求直线DB1与BC所成角的大小.(结果用反三角函教值表示)
如图,圆柱底面直径为10,母线BB1=6,矩形ABCD内接于圆柱的下底面,BC=6,求直线DB1与BC所成角的大小.(结果用反三角函教值表示) 分析 以B为坐标原点,BC,BA,BB1方向分别为x,y,z轴正方向,建立空间坐标系,分别求出直线DB1与BC的方向向量,代入向量夹角公式,可得答案.
解答 解:∵圆柱底面直径为10,即BD=10,BC=6,故AB=$\sqrt{{10}^{2}-{6}^{2}}$=8,
以B为坐标原点,BC,BA,BB1方向分别为x,y,z轴正方向,建立空间坐标系,
由母线BB1=6,可得:B(0,0,0),C(6,0,0),D(6,8,0),B1(0,0,6),
∴$\overrightarrow{{DB}_{1}}$=(-6,-8,6),$\overrightarrow{BC}$=(6,0,0),
设直线DB1与BC所成角的大小为θ,
则cosθ=$\frac{|\overrightarrow{{DB}_{1}}•\overrightarrow{BC}|}{\left|\overrightarrow{{DB}_{1}}\right|•\left|\overrightarrow{BC}\right|}$=$\frac{36}{24\sqrt{34}}$=$\frac{3\sqrt{34}}{68}$,
故直线DB1与BC所成角的大小为arccos$\frac{3\sqrt{34}}{68}$
点评 本题考查的知识点是异面直线所成的角,建立空间坐标系,将异面直线夹角转化为向量夹角,是解答的关键.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | 72 | B. | 24 | C. | 36 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com