
分析 令t=9-x2>0,求得函数的定义域为(-3,3),由y=log${\;}_{\frac{1}{3}}$t为减函数,故复合函数的单调递增区间,即为内函数的单调递减区间.
解答 解:令t=9-x2>0,求得-3<x<3,故函数的定义域为(-3,3),
则y=log${\;}_{\frac{1}{3}}$t,
∵y=log${\;}_{\frac{1}{3}}$t为减函数,
t=9-x2在(-3,0]上为增函数,在[0,3)上为减函数,
故函数f(x)=log${\;}_{\frac{1}{3}}$(9-x2)的单调增区间为[0,3),
故答案为:[0,3)
点评 本题主要考查对数函数、二次函数的性质,复合函数的单调性,体现了转化的数学思想,属于基础题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
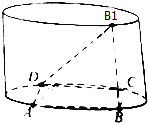 如图,圆柱底面直径为10,母线BB1=6,矩形ABCD内接于圆柱的下底面,BC=6,求直线DB1与BC所成角的大小.(结果用反三角函教值表示)
如图,圆柱底面直径为10,母线BB1=6,矩形ABCD内接于圆柱的下底面,BC=6,求直线DB1与BC所成角的大小.(结果用反三角函教值表示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com