
分析 (1)当n=1时,当n=2时,即可求解a1,a2.
(2)由题设求出S1=$\frac{1}{2}$,S2=$\frac{2}{3}$.S3=$\frac{3}{4}$.由此猜想Sn=$\frac{n}{n+1}$,n=1,2,3,….然后用数学归纳法证明这个结论.
解答 解:(1)当n=1时,x2-a1x-a1=0有一根为S1-1=a1-1,
于是(a1-1)2-a1(a1-1)-a1=0,解得a1=$\frac{1}{2}$.
当n=2时,x2-a2x-a2=0有一根为S2-1=a2-$\frac{1}{2}$,
于是(a2-$\frac{1}{2}$)2-a2(a2-$\frac{1}{2}$)-a2=0,
解得a2=$\frac{1}{6}$
(2)由题设(Sn-1)2-an(Sn-1)-an=0,
S${\;}_{n}^{2}$-2Sn+1-anSn=0.
当n≥2时,an=Sn-Sn-1,
代入上式得Sn-1Sn-2Sn+1=0.①
由(1)得S1=a1=$\frac{1}{2}$,S2=a1+a2=$\frac{1}{2}$+$\frac{1}{6}$=$\frac{2}{3}$.
由①可得S3=$\frac{3}{4}$.由此猜想Sn=$\frac{n}{n+1}$,n=1,2,3,….
下面用数学归纳法证明这个结论.
(i)n=1时已知结论成立.
(ii)假设n=k时结论成立,即Sk=$\frac{k}{k+1}$,
当n=k+1时,由①得Sk+1=$\frac{1}{2-Sk}$,即Sk+1=$\frac{k+1}{k+2}$,故n=k+1时结论也成立.
综上,由(i)、(ii)可知Sn=$\frac{n}{n+1}$对所有正整数n都成立.
点评 本题考查数列的综合应用,数学归纳法的应用,考查逻辑推理能力以及计算能力.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 72 | B. | 24 | C. | 36 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | i | D. | -i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
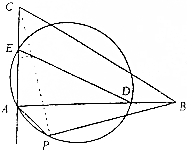 如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.
如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com