Question

2．在四棱锥P-ABCD中，四边形ABCD是梯形，AD∥BC，∠ABC=90°，平面PAB⊥平面ABCD，平面 PAD⊥平面ABCD．
（1）求证：PA⊥平面ABCD：
（2）若平面PAB∩平面PCD=l，问：直线l能否与平面ABCD平行？请说明理由．

Answer 1

分析 （1）根据面面垂直的性质定理，可得AB⊥平面 PAD，进而AB⊥PA，及AD⊥PA，再利用线面垂直的判定定理，得到结论；
（2）若平面PAB∩平面PCD=l，则直线l与平面ABCD不平行，利用反证法，结合线面平行的性质定理，可得结论；

解答 证明：（1）∵AD∥BC，∠ABC=90°，
∴∠BAD=90°，即AB⊥AD，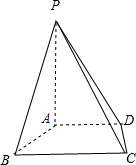

∵平面 PAD⊥平面ABCD，平面 PAD∩平面ABCD=AD，AB?平面ABCD，
∴AB⊥平面 PAD，进而AB⊥PA，
同理由平面PAB⊥平面ABCD可得AD⊥PA，
又∵AD∩AD=A，AB，AD?平面ABCD，
∴PA⊥平面ABCD：
（2）若平面PAB∩平面PCD=l，则直线l与平面ABCD不平行，理由如下：
假定直线l∥平面ABCD，
由于l?平面PCD，且平面PCD∩平面ABCD=CD，所以l∥CD，
同理可得l∥AB，
所以AB∥CD，
这与AB和CD是直角梯形ABCD的两腰相矛盾，
故假设错误，所以直线l与平面ABCD不平行．

点评 本题考查的知识点是面面垂直的性质定理，线面垂直的判定定理，线面平行的性质定理，反证法，难度中档．