
| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{7}$ |
分析 用不等式表示出a,b满足的关系,分别求出对应区域的面积,利用几何概型的概率公式即可得到结论.
解答 解:在区间[0,1]上随机地任取两个数a,b,则a,b对应的区域面积为1×1=1,
满足a<b<$\sqrt{a}$的区域面积为${∫}_{0}^{1}(\sqrt{a}-a)da$=($\frac{2}{3}{a}^{\frac{3}{2}}$-$\frac{1}{2}{a}^{2}$)${|}_{0}^{1}$=$\frac{1}{6}$,
∴满足a<b<$\sqrt{a}$的概率是$\frac{1}{6}$.
故选:C.
点评 本题主要考查几何概型的计算,利用不等式对应的平面区域,求出相应的面积是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
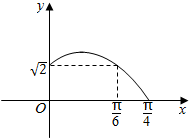 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com