
分析 ①令m=|$\overrightarrow{a}$+t$\overrightarrow{b}$|,$\overrightarrow{a}$,$\overrightarrow{b}$夹角为θ,对m2进行变形,然后利用二次函数的性质可得其取最小值时t的值;
②当$\overrightarrow{a}$与$\overrightarrow{b}$成45°角,cosθ=$\frac{\sqrt{2}}{2}$,只需证明$\overrightarrow{b}$•($\overrightarrow{a}$+t$\overrightarrow{b}$)=0即可.
解答 解:①令m=|$\overrightarrow{a}$+t$\overrightarrow{b}$(t∈R),${\overrightarrow{m}}^{2}={\overrightarrow{a}}^{2}+{t}^{2}{\overrightarrow{b}}^{2}+2t|\overrightarrow{a}|•|\overrightarrow{b}|cosθ$,
所以当t=-$\frac{|\overrightarrow{a}|cosθ}{|\overrightarrow{b}|}$时,mmin=|$\overrightarrow{a}$|sinθ;
②证明:因为$\overrightarrow{a}$与$\overrightarrow{b}$成45°角,
t=-$\frac{\sqrt{2}}{2}\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$,
所以$\overrightarrow{b}$•($\overrightarrow{a}$+t$\overrightarrow{b}$)=$\overrightarrow{a}•\overrightarrow{b}+t{\overrightarrow{b}}^{2}$=$\frac{\sqrt{2}}{2}|\overrightarrow{a}||\overrightarrow{b}|$-$\frac{\sqrt{2}}{2}\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}×|\overrightarrow{b}{|}^{2}$=0,
所以$\overrightarrow{b}$与$\overrightarrow{a}$+t$\overrightarrow{b}$(t∈R)垂直;
点评 本题考查利用平面向量的数量积证明向量垂直,属基础题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:填空题
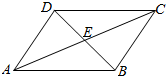 如图,在平行四边形ABCD中,$\overrightarrow{AE}$=x$\overrightarrow{AD}$+y$\overrightarrow{AB}$,则x+y=1.
如图,在平行四边形ABCD中,$\overrightarrow{AE}$=x$\overrightarrow{AD}$+y$\overrightarrow{AB}$,则x+y=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com