
分析 求出P的轨迹方程,A、B满足的轨迹方程,利用|PA|-|PB|的几何意义求出最大值即可.
解答 解:点p、A、B依次是满足|z-1|=2Rez-$\frac{1}{2}$、|z+1|=1、|z-1|=$\frac{1}{4}$的复数z在复平面上对应的点,
可知P,满足(x-1)2+y2=(2x-$\frac{1}{2}$)2;可得:3x2-y2=$\frac{3}{4}$,即$\frac{{x}^{2}}{\frac{1}{4}}-\frac{{y}^{2}}{\frac{3}{4}}=1$.焦点坐标(-1,0),(1,0)
A满足:(x+1)2+y2=1,圆心F1(-1,0),半径为1.
B满足:(x-1)2+y2=$\frac{1}{16}$,圆心F2(1,0)半径为$\frac{1}{4}$.
|PA|-|PB|的最大值为:|PF1|+1-|PF2|-$\frac{1}{4}$=1+1-$\frac{1}{4}$=$\frac{7}{4}$.
故答案为:$\frac{7}{4}$.
点评 本题考查复数的代数表示法及其几何意义,考查数形结合的解题思想方法,关键是对题意的理解,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,1-2$\sqrt{3}$)∪(2$\sqrt{3}$+1,+∞) | B. | [2$\sqrt{3}$-1,+∞) | ||
| C. | (-∞,-1-2$\sqrt{3}$]∪[2$\sqrt{3}$-1,+∞) | D. | (-∞,-1-2$\sqrt{3}$]∪[2$\sqrt{3}$+1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | q=$\frac{a+b}{2}$ | B. | q≥$\frac{a+b}{2}$ | ||
| C. | q≤$\frac{a+b}{2}$ | D. | q与$\frac{a+b}{2}$的大小关系不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
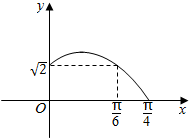 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com