
已知函数 .
.
(1)当 时,求函数
时,求函数 的极值;
的极值;
(2)设定义在D上的函数 在点
在点 处的切线方程为
处的切线方程为 .当
.当 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数 的“转点”.当
的“转点”.当 时,试问函数
时,试问函数 是否存在“转点”?若存在,求出“转点”的横坐标;若不存在,请说明理由.
是否存在“转点”?若存在,求出“转点”的横坐标;若不存在,请说明理由.
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
已知函数y=f(x)的导函数y=f′(x)的图象如图,则( )
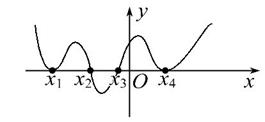 A.函数f(x)有1个极大值点,1个极小值点
A.函数f(x)有1个极大值点,1个极小值点
B.函数f(x)有2个极大值点,2个极小值点
C.函数f(x)有3个极大值点,1个极小值点
D.函数f(x)有1个极大值点,3个极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
将容量为n的样本中的数据分成6组,绘制成频率分布直方图,若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频数之和等于27,则n等于______________
查看答案和解析>>
科目:高中数学 来源: 题型:
若直线 同时平分一个三角形的周长和面积,则称直线
同时平分一个三角形的周长和面积,则称直线 为该三角形的“平分线”,已知△ABC三边之长分别为3,4,5,则△ABC的“平分线”的条数为
为该三角形的“平分线”,已知△ABC三边之长分别为3,4,5,则△ABC的“平分线”的条数为
A.1 B.0 C.3 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com