
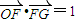 ,设
,设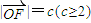 ,
,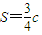 .
.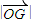 取最小值时,求椭圆E的标准方程.
取最小值时,求椭圆E的标准方程.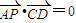 ,试求CD直线方程.
,试求CD直线方程.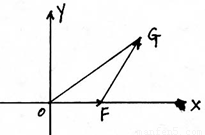
 c•|y|=
c•|y|= c即可求得点G的纵坐标;
c即可求得点G的纵坐标;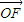 •
•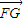 =c(x-c)=1,可求得x=c+
=c(x-c)=1,可求得x=c+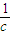 ,从而可求得|
,从而可求得|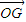 |=
|=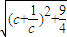 (c≥2),构造函数f(c)=c+
(c≥2),构造函数f(c)=c+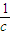 ,利用其单调性质可求得当c=2时f(c)有最小值
,利用其单调性质可求得当c=2时f(c)有最小值 ,从而可求得G点坐标;
,从而可求得G点坐标;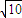 ,0),B(
,0),B(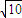 ,0),C(0,-
,0),C(0,-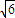 ),由设P(x1,y1),可求得kAP•kBP=-
),由设P(x1,y1),可求得kAP•kBP=-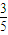 ,继而可求得kAP=-
,继而可求得kAP=-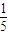 ,再由
,再由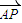 •
•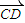 =0可求得kCD=5,从而可求得直线CD的方程.
=0可求得kCD=5,从而可求得直线CD的方程. |
|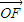 |•|y|,
|•|y|, c=
c= c•|y|,|y|=
c•|y|,|y|= ,
, =(c,0),
=(c,0),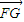 =(x-c,y)(y>0),
=(x-c,y)(y>0), …(3分)
…(3分)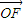 •
•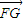 =c(x-c)=1,∴x=c+
=c(x-c)=1,∴x=c+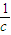
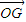 |=
|=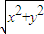 =
=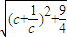 (c≥2)
(c≥2) 在[2,+∞]上递增,
在[2,+∞]上递增, =
= ,
, ,y=
,y= ,
, ,
, ),
),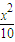 +
+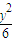 =1…(8分)
=1…(8分)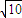 ,0),B(
,0),B(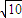 ,0),C(0,-
,0),C(0,-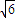 ),
),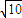 经过点B,
经过点B,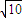
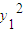 =
=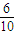 (10-
(10-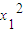 ),
),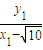 ×
×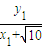 =
=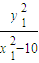
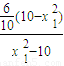 =-
=-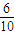 =-
=-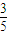 ,
,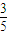 ×
×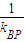 =-
=-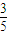 •
•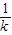 =-
=-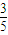 •
• =-
=-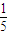 ,
,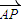 •
•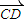 =0,
=0,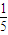 •kCD=-1,
•kCD=-1,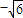 )故:所求CD方程为:y=5x-
)故:所求CD方程为:y=5x-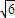 …(13分)
…(13分)

科目:高中数学 来源: 题型:
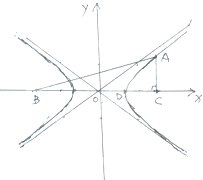 如图,直角坐标系xoy中,有Rt△ABC,∠C=90°,D在边BC上,BD=3DC,双曲线E以B、C为焦点,且经过A、D两点.
如图,直角坐标系xoy中,有Rt△ABC,∠C=90°,D在边BC上,BD=3DC,双曲线E以B、C为焦点,且经过A、D两点.查看答案和解析>>
科目:高中数学 来源: 题型:
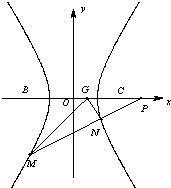 如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.
如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.| MP |
| PN |
| BC |
| GM |
| GN |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•芜湖二模)如图,直角坐标系XOY中,点F在x轴正半轴上,△OFG的面积为S.且
(2012•芜湖二模)如图,直角坐标系XOY中,点F在x轴正半轴上,△OFG的面积为S.且| OF |
| FG |
| OF |
| 3 |
| 4 |
| OG |
| AP |
| CD |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•蓝山县模拟)如图,直角坐标系xOy中,一直角三角形ABC,∠=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.
(2012•蓝山县模拟)如图,直角坐标系xOy中,一直角三角形ABC,∠=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.| MP |
| PN |
| BC |
| GM |
| GN |
查看答案和解析>>
科目:高中数学 来源: 题型:
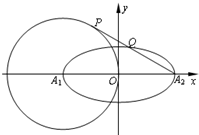 如图平面直角坐标系xOy中,椭圆
如图平面直角坐标系xOy中,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| PQ |
| QA2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com