
分析 根据数列的递推关系得到2an+1=an,即数列{an}是公比q=$\frac{1}{2}$,首项为a1=3的等比数列,结合等比数列的通项公式进行求解即可.
解答 解:∵a1=3,4Sn+1=6an+1-an+4Sn,
∴4Sn+1-4Sn=6an+1-an,
即4an+1=6an+1-an,
即2an+1=an,
则$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{1}{2}$,
则数列{an}是公比q=$\frac{1}{2}$,首项为a1=3的等比数列,
则数列的通项公式为an=3•($\frac{1}{2}$)n-1,n∈N•,
故答案为:an=3•($\frac{1}{2}$)n-1,n∈N•
点评 本题主要考查数列通项公式的求解,利用数列的递推关系判断数列是等比数列是解决本题的关键.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:选择题
| A. | b=a2或a=b2 | B. | a=b-1或a=b3 | C. | a=b-1或b=a3 | D. | a=b3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
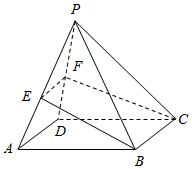 已知四棱锥P-ABCD的底面为平行四边形,高为h,过底面一边BC作截面,与侧面PAQ交于EF,若截面将棱锥分成体积相等的两部分,
已知四棱锥P-ABCD的底面为平行四边形,高为h,过底面一边BC作截面,与侧面PAQ交于EF,若截面将棱锥分成体积相等的两部分,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
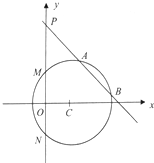 已知圆心在x轴正半轴上的圆C与直线5x+12y+21=0相切,与y轴交于M,N两点,且∠MCN=120°.
已知圆心在x轴正半轴上的圆C与直线5x+12y+21=0相切,与y轴交于M,N两点,且∠MCN=120°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com