
分析 如图点P到准线的距离等于点P到焦点F的距离,过焦点F作直线4x-3y+8=0的垂线,此时d1+d2最小,根据抛物线方程求得F,进而利用点到直线的距离公式求得d1+d2的最小值.
解答 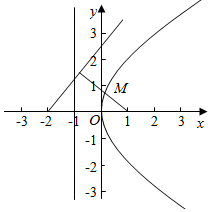 解:抛物线y2=4x的焦点坐标(1,0),准线方程为:x=-1,
解:抛物线y2=4x的焦点坐标(1,0),准线方程为:x=-1,
如图点M到准线的距离等于点P到焦点F的距离,
过焦点F作直线4x-3y+8=0的垂线,此时d1+d2最小.
∵F(1,0),则d1+d2=$\frac{|4+8|}{\sqrt{{4}^{2}+(-3)^{2}}}$-1=$\frac{7}{5}$,
故答案为:$\frac{7}{5}$.
点评 本题主要考查了抛物线的简单性质,两点距离公式的应用.解此类题设宜先画出图象,进而利用数形结合的思想解决问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | 10 | 27 | 37 |
| 不赞成 | 10 | 3 | 13 |
| 合计 | 20 | 30 | 50 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com