
分析 (Ⅰ)由x=ρcosθ,y=ρsinθ,代入曲线C的极坐标方程,可得曲线的直角坐标方程,联立直线l的方程,消去y,运用判别式大于等于0,可得斜率的范围,再由斜率公式,可得倾斜角的范围;
(Ⅱ)求得曲线C的参数方程,运用两角和的正弦公式和正弦函数的值域,即可得到所求范围.
解答 解:(Ⅰ)曲线C的极坐标方程转化成直角坐标方程是C:x2+y2-6x+5=0,
由题意知直线l的斜率存在,设直线l:y=k(x+1),其中k=tanα.
联立$\left\{\begin{array}{l}{x^2}+{y^2}-6x+5=0\;,\;\;\\ y=k(x+1)\;,\;\;\end{array}\right.$
消去y得(1+k2)x2+2(k2-3)x+k2+5=0.
因为直线l和曲线C有交点,所以△=4(k2-3)2-4(1+k2)(k2+5)≥0,
即$-\frac{{\sqrt{3}}}{3}≤k≤\frac{{\sqrt{3}}}{3}$,
即$tanα∈[-\frac{{\sqrt{3}}}{3}\;,\;\;\frac{{\sqrt{3}}}{3}]$,
所以$α∈[0\;,\;\;\frac{π}{6}]∪[\frac{5π}{6}\;,\;\;π)$.
(Ⅱ)曲线C:x2+y2-6x+5=0即(x-3)2+y2=4的参数方程是$\left\{\begin{array}{l}x=3+2cosθ\;,\;\;\\ y=2sinθ\;,\;\;\end{array}\right.$(θ为参数),
所以点B(x,y)的坐标可以写成(3+2cosθ,2sinθ),
所以$\sqrt{3}x+y=3\sqrt{3}+2sinθ+2\sqrt{3}cosθ=3\sqrt{3}+4sin(θ+\frac{π}{3})$,
因为sin(θ+$\frac{π}{3}$)∈[-1,1],
所以$\sqrt{3}$x+y∈[3$\sqrt{3}$-4,3$\sqrt{3}$+4].
点评 本题考查极坐标方程和直角坐标方程的互化,直线和圆的位置关系的判断和应用,注意运用转化思想和判别式大于等于0,考查圆的参数方程的运用和两角和的正弦公式及正弦函数的值域的运用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
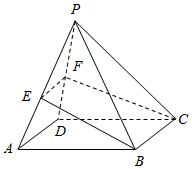 已知四棱锥P-ABCD的底面为平行四边形,高为h,过底面一边BC作截面,与侧面PAQ交于EF,若截面将棱锥分成体积相等的两部分,
已知四棱锥P-ABCD的底面为平行四边形,高为h,过底面一边BC作截面,与侧面PAQ交于EF,若截面将棱锥分成体积相等的两部分,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
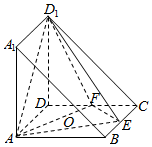 如图,在直三棱柱ABA1-DCD1中,${D_1}C=\sqrt{2}a$,DD1=DA=DC=a,点E、F分别是BC、DC的中点.
如图,在直三棱柱ABA1-DCD1中,${D_1}C=\sqrt{2}a$,DD1=DA=DC=a,点E、F分别是BC、DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com