
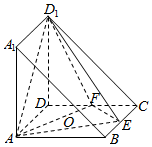
 如图,在直三棱柱ABA1-DCD1中,${D_1}C=\sqrt{2}a$,DD1=DA=DC=a,点E、F分别是BC、DC的中点.
如图,在直三棱柱ABA1-DCD1中,${D_1}C=\sqrt{2}a$,DD1=DA=DC=a,点E、F分别是BC、DC的中点.分析 法一:(I)由已知得$D{D_1}^2+D{C^2}={D_1}{C^2}$,DD1⊥DC.利用线面垂直的判定定理可得DD1⊥平面ABCD.于是DD1⊥AF.由已知可得△ADF≌△CDE,得到AF⊥DE.即可证明AF⊥平面D1DE,AF⊥ED1.
(Ⅱ)设三棱锥D1-AEF的体积为V,点E到平面AFD1的距离为h,利用${V}_{{D}_{1}-AEF}$=${V}_{E-A{D}_{1}F}$即可得出.
法二:(I)由已知得$D{D_1}^2+D{C^2}={D_1}{C^2}$,可得DD1⊥DC.如图所示,建立空间直角坐标系.计算$\overrightarrow{AF}$•$\overrightarrow{{D}_{1}E}$=0,即可证明$\overrightarrow{AF}$⊥$\overrightarrow{{D}_{1}E}$.
(II)设平面AD1F的法向量为$\overrightarrow{n}$=(x,y,z),可得$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AF}=0}\\{\overrightarrow{n}•\overrightarrow{A{D}_{1}}=0}\end{array}\right.$,解得$\overrightarrow{n}$,可得点E到平面AFD1的距离d=$\frac{|\overrightarrow{n}•\overrightarrow{AE}|}{|\overrightarrow{n}|}$.
解答 法一:(I)证明:由已知得$D{D_1}^2+D{C^2}={D_1}{C^2}$,DD1⊥DC.
连接DE,由已知得AD⊥DD1,又DD1⊥DC,AD∩DC=D,∴DD1⊥平面ABCD.
又AF?平面ABCD,∴DD1⊥AF.
DA=DC=a,$CE=DF=\frac{1}{2}a$,∠ADF=∠DCE=90°,△ADF≌△CDE,∠DAF=∠CDE,AF⊥DE.
又DD1∩DE=D,∴AF⊥平面D1DE,AF⊥ED1.
(Ⅱ)设三棱锥D1-AEF的体积为V,点E到平面AFD1的距离为h,$V=\frac{1}{3}×{S_{△AEF}}×D{D_1}=\frac{1}{3}×({a^2}-2×\frac{1}{2}×\frac{1}{2}a×a-\frac{1}{2}×\frac{1}{2}a×\frac{1}{2}a)×a=\frac{1}{8}{a^3}$,
${D_1}F=AF=\frac{{\sqrt{5}}}{2}a$,$A{D_1}=\sqrt{2}a$,
过F作FG⊥AD1于G,则$FG=\frac{{\sqrt{3}}}{2}a$,△AD1F的面积$S=\frac{{\sqrt{6}}}{4}{a^2}$,
∴$\frac{1}{3}×\frac{{\sqrt{6}}}{4}{a^2}×h=\frac{1}{8}{a^3}$,解得$h=\frac{{\sqrt{6}}}{4}a$.)
法二:(I)证明:由已知得$D{D_1}^2+D{C^2}={D_1}{C^2}$,∴DD1⊥DC.
如图所示,建立空间直角坐标系.D(0,0,0),A(a,0,0),C(0,a,0),B(a,a,0),E($\frac{a}{2}$,a,0),F(0,$\frac{a}{2}$,0),
D1(0,0,a).
$\overrightarrow{AF}$=$(-a,\frac{a}{2},0)$,$\overrightarrow{{D}_{1}E}$=$(\frac{a}{2},a,-a)$.
∵$\overrightarrow{AF}$•$\overrightarrow{{D}_{1}E}$=-$\frac{{a}^{2}}{2}$+$\frac{{a}^{2}}{2}$+0=0,∴$\overrightarrow{AF}$⊥$\overrightarrow{{D}_{1}E}$.
∴AF⊥ED1.
(II)解:$\overrightarrow{A{D}_{1}}$=(-a,0,a),$\overrightarrow{AE}$=$(-\frac{a}{2},a,0)$.
设平面AD1F的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AF}=0}\\{\overrightarrow{n}•\overrightarrow{A{D}_{1}}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{-ax+\frac{a}{2}y=0}\\{-ax+az=0}\end{array}\right.$,
取$\overrightarrow{n}$=(1,2,1),
∴点E到平面AFD1的距离d=$\frac{|\overrightarrow{n}•\overrightarrow{AE}|}{|\overrightarrow{n}|}$=$\frac{|-\frac{a}{2}+2a|}{\sqrt{6}}$=$\frac{\sqrt{6}}{4}a$.
点评 本题考查了空间位置关系、距离的计算、线面垂直判定与性质定理、等体积法、法向量的应用、相互垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
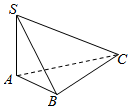 如图,三棱锥S-ABC中,SA⊥平面ABC,AB=6,BC=12,AC=6$\sqrt{5}$.SB=6$\sqrt{2}$,则三棱锥S-ABC外接球的表面积为216π.
如图,三棱锥S-ABC中,SA⊥平面ABC,AB=6,BC=12,AC=6$\sqrt{5}$.SB=6$\sqrt{2}$,则三棱锥S-ABC外接球的表面积为216π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com