
分析 (1)求得不等式f(x+$\frac{1}{2}$)≥2m+1(m>0)的解集,再结合不等式f(x+$\frac{1}{2}$)≥2m+1(m>0)的解集为(-∞,-2]∪[2,+∞),求得m的值.
(2)由题意可得g(x)=|2x-1|-|2x+3|的最小值小于或等于2y+$\frac{a}{{2}^{y}}$,再利用绝对值三角不等式求得g(x)的最小值为4,可得4≤2y+$\frac{a}{{2}^{y}}$ 恒成立,再利用基本不等式求得2y+$\frac{a}{{2}^{y}}$ 的最小值为2$\sqrt{a}$,可得2$\sqrt{a}$≥4,从而求得a的范围.
解答 解:(1)∵不等式f(x+$\frac{1}{2}$)≥2m+1(m>0)的解集为(-∞,-2]∪[2,+∞),
即|2(x+$\frac{1}{2}$)-1|≤2m+1 的解集为(-∞,-2]∪[2,+∞).
由|2x|≥2m+1,可得2x≥2m+1,或2x≤-2m-1,
求得 x≥m+$\frac{1}{2}$,或x≤-m-$\frac{1}{2}$,
故|2(x+$\frac{1}{2}$)-1|≤2m+1 的解集为(-∞,-m-$\frac{1}{2}$]∪[m+$\frac{1}{2}$,+∞),
故有m+$\frac{1}{2}$=2,且-m-$\frac{1}{2}$=-2,
∴m=$\frac{3}{2}$.
(2)∵不等式f(x)≤2y+$\frac{a}{{2}^{y}}$+|2x+3|,对任意的实数x,y∈R恒成立,
∴|2x-1|≤2y+$\frac{a}{{2}^{y}}$+|2x+3|恒成立,
即|2x-1|-|2x+3|≤2y+$\frac{a}{{2}^{y}}$ 恒成立,
故g(x)=|2x-1|-|2x+3|的最小值小于或等于2y+$\frac{a}{{2}^{y}}$.
∵|2x-1|-|2x+3|≤|2x-1-(2x+3)|=4,
∴4≤2y+$\frac{a}{{2}^{y}}$ 恒成立,
∵2y+$\frac{a}{{2}^{y}}$≥2$\sqrt{a}$,
∴2$\sqrt{a}$≥4,
∴a≥4,
故实数a的最小值为4.
点评 本题主要考查绝对值的意义,绝对值不等式的解法,函数的恒成立问题,体现了转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
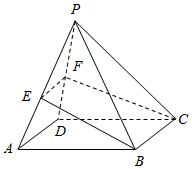 已知四棱锥P-ABCD的底面为平行四边形,高为h,过底面一边BC作截面,与侧面PAQ交于EF,若截面将棱锥分成体积相等的两部分,
已知四棱锥P-ABCD的底面为平行四边形,高为h,过底面一边BC作截面,与侧面PAQ交于EF,若截面将棱锥分成体积相等的两部分,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
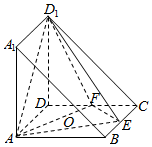 如图,在直三棱柱ABA1-DCD1中,${D_1}C=\sqrt{2}a$,DD1=DA=DC=a,点E、F分别是BC、DC的中点.
如图,在直三棱柱ABA1-DCD1中,${D_1}C=\sqrt{2}a$,DD1=DA=DC=a,点E、F分别是BC、DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com