
分析 直线ax+by=1与线段AB有一个公共点,可知:点A(1,0),B(2,1)在直线ax+by=1的两侧,因此(a-1)(2a+b-1)≤0.画出它们表示的平面区域,如图所示.由图可知,当原点O到直线2x+y-1=0的距离为原点到区域内的点的距离的最小值,可得dmin=$\frac{1}{\sqrt{5}}$.由于存在实数a、b使得不等式$\frac{1}{si{n}^{2}θ}$+$\frac{p}{co{s}^{2}θ}$≥20(a2+b2)对于任意θ∈(0,$\frac{π}{2}$)成立,可得$(\frac{1}{si{n}^{2}θ}+\frac{p}{co{s}^{2}θ})_{min}$≥20(a2+b2)min=4,再利用基本不等式的性质即可得出答案.
解答 解:∵直线ax+by=1与线段AB有一个公共点,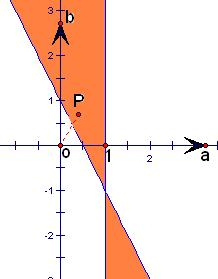
∴点A(1,0),B(2,1)在直线ax+by=1的两侧,
∴(a-1)(2a+b-1)≤0,
即 $\left\{\begin{array}{l}{a-1≤0}\\{2a+b-1≥0}\end{array}\right.$,或$\left\{\begin{array}{l}{a-1≥0}\\{2a+b-1≤0}\end{array}\right.$;
画出它们表示的平面区域,如图所示.
a2+b2表示原点到区域内的点的距离的平方,
由图可知,当原点O到直线2x+y-1=0的距离为原点到区域内的点的距离的最小值,
∵dmin=$\frac{1}{\sqrt{5}}$
那么a2+b2的最小值为:d2=$\frac{1}{5}$.
由于存在实数a、b使得不等式$\frac{1}{si{n}^{2}θ}$+$\frac{p}{co{s}^{2}θ}$≥20(a2+b2)对于任意θ∈(0,$\frac{π}{2}$)成立,
∴$(\frac{1}{si{n}^{2}θ}+\frac{p}{co{s}^{2}θ})_{min}$≥20(a2+b2)min=4,
∵θ∈(0,$\frac{π}{2}$),∴sinθ,cosθ∈(0,1).
∴$\frac{1}{si{n}^{2}θ}$+$\frac{p}{co{s}^{2}θ}$=(sin2θ+cos2θ)$(\frac{1}{si{n}^{2}θ}+\frac{p}{co{s}^{2}θ})$=1+p+$\frac{co{s}^{2}θ}{si{n}^{2}θ}$+$\frac{psi{n}^{2}θ}{co{s}^{2}θ}$≥1+p+2$\sqrt{\frac{co{s}^{2}θ}{si{n}^{2}θ}•\frac{psi{n}^{2}θ}{co{s}^{2}θ}}$=1+p+2$\sqrt{p}$,
当且仅当tan2θ=$\frac{1}{\sqrt{p}}$时取等号.
∴1+p+2$\sqrt{p}$≥4,p>0,解得1≤p.
∴tanθ=1,即$θ=\frac{π}{4}$时取等号.
故答案为:[1,+∞).
点评 本题考查了函数图象与性质、线性规划有关知识、三角函数基本关系式、基本不等式的性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
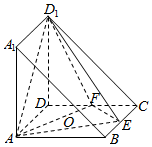 如图,在直三棱柱ABA1-DCD1中,${D_1}C=\sqrt{2}a$,DD1=DA=DC=a,点E、F分别是BC、DC的中点.
如图,在直三棱柱ABA1-DCD1中,${D_1}C=\sqrt{2}a$,DD1=DA=DC=a,点E、F分别是BC、DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com