
分析 (1)由代入消元法,可得直线的普通方程;运用x=ρcosθ,y=ρsinθ,可得曲线C的普通方程;
(2)求得直线l的标准参数方程,代入曲线C的普通方程,可得二次方程,运用韦达定理和参数的几何意义,即可得到所求和.
解答 解:(1)直线l:$\left\{\begin{array}{l}{x=1+t}\\{y=-2+t}\end{array}\right.$(t为参数),
消去t,可得直线l的普通方程为x-y-3=0;
曲线C的极坐标方程为ρsin2θ=2cosθ,
即为ρ2sin2θ=2ρcosθ,
由x=ρcosθ,y=ρsinθ,可得
曲线C的普通方程为y2=2x;
(2)直线l的标准参数方程为$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}m}\\{y=-2+\frac{\sqrt{2}}{2}m}\end{array}\right.$(m为参数),
代入曲线C:y2=2x,
可得m2-6$\sqrt{2}$m+4=0,即有m1+m2=6$\sqrt{2}$,m1m2=4,
则|PA|+|PB|=|m1|+|m2|=m1+m2=6$\sqrt{2}$.
点评 本题考查极坐标方程和直角坐标方程的互化、参数方程和普通方程的互化,考查直线的参数方程的运用,注意运用联立方程和韦达定理,以及参数的几何意义,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:填空题
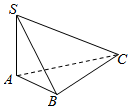 如图,三棱锥S-ABC中,SA⊥平面ABC,AB=6,BC=12,AC=6$\sqrt{5}$.SB=6$\sqrt{2}$,则三棱锥S-ABC外接球的表面积为216π.
如图,三棱锥S-ABC中,SA⊥平面ABC,AB=6,BC=12,AC=6$\sqrt{5}$.SB=6$\sqrt{2}$,则三棱锥S-ABC外接球的表面积为216π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第7幅图的蜂巢总数为( )
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第7幅图的蜂巢总数为( )| A. | 61 | B. | 90 | C. | 91 | D. | 127 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com