
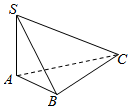
 如图,三棱锥S-ABC中,SA⊥平面ABC,AB=6,BC=12,AC=6$\sqrt{5}$.SB=6$\sqrt{2}$,则三棱锥S-ABC外接球的表面积为216π.
如图,三棱锥S-ABC中,SA⊥平面ABC,AB=6,BC=12,AC=6$\sqrt{5}$.SB=6$\sqrt{2}$,则三棱锥S-ABC外接球的表面积为216π. 分析 由SA⊥平面ABC,可得SA⊥AB,SA的长度.由于AB2+BC2=AC2,可得∠ABC=90°.可把此三棱锥补成长方体,其外接球的直径为SC的长.
解答 解:∵SA⊥平面ABC,∴SA⊥AB.∴SA=$\sqrt{S{B}^{2}-A{B}^{2}}$=6.
∵AB2+BC2=62+122=180=$(6\sqrt{5})^{2}$=AC2,∴∠ABC=90°
可把此三棱锥补成长方体,其外接球的直径为SC的长.
SC2=SA2+AC2=${6}^{2}+(6\sqrt{5})^{2}$=216,解得SC=$6\sqrt{6}$,
∴2R=6$\sqrt{6}$,解得R=3$\sqrt{6}$.
故所求的外接球的表面积S=4πR2=4π×$(3\sqrt{6})^{2}$=216π.
故答案为:216π .
.
点评 本题考查了三棱锥与长方体的外接球、勾股定理及其逆定理、球的表面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰直角三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.
已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰直角三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
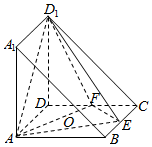 如图,在直三棱柱ABA1-DCD1中,${D_1}C=\sqrt{2}a$,DD1=DA=DC=a,点E、F分别是BC、DC的中点.
如图,在直三棱柱ABA1-DCD1中,${D_1}C=\sqrt{2}a$,DD1=DA=DC=a,点E、F分别是BC、DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=13,n=20 | B. | m=14,n=20 | C. | m=20,n=20 | D. | m=20,n=30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,e${\;}^{\frac{1}{e}}}$) | B. | (1,e] | C. | (1,e2) | D. | (e${\;}^{\frac{1}{e}}}$,e2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com