
| A. | (1,e${\;}^{\frac{1}{e}}}$) | B. | (1,e] | C. | (1,e2) | D. | (e${\;}^{\frac{1}{e}}}$,e2) |
分析 由f(x)=0得ax=logax,构造函数f(x)=ax与g(x)=logax,关于y=x对称,只需要讨论与y=x有两个解即可,构造函数h(x)=ax-x,求函数的导数,只须h(x)的最小值小于0,即可.
解答 解:由f(x)=0得ax=logax,
设函数f(x)=ax与g(x)=logax,则两个函数关于y=x对称,只需要讨论与y=x有两个解即可,
令h(x)=ax-x,则函数h(x)有两个零点,
当0<a<1时,函数h(x)为减函数,至多有一个零点不满足要求,
当a>1时,令h′(x)=axlna-1=0,则x=${log}_{a}\frac{1}{lna}$,
当0<x<${log}_{a}\frac{1}{lna}$时,h′(x)<0,此时函数h(x)为减函数;
当x>${log}_{a}\frac{1}{lna}$时,h′(x)>0,此时函数h(x)为增函数;
故当x=${log}_{a}\frac{1}{lna}$时,函数h(x)取最小值
若函数h(x)有两个零点,则h(${log}_{a}\frac{1}{lna}$)<0,
即${a}^{{log}_{a}\frac{1}{lna}}<{log}_{a}\frac{1}{lna}$,
即$\frac{1}{lna}={log}_{a}e<{log}_{a}\frac{1}{lna}$,
即$e<\frac{1}{lna}$,
即$0<lna<\frac{1}{e}$,
即$1<a<{e}^{\frac{1}{e}}$,
故实数a的取值范围是(1,e${\;}^{\frac{1}{e}}$),
故选:A
点评 本题考查的知识点是根的存在性及根的个数判断,反函数,导数法判断函数的单调性,导数法求函数的最值,涉及的知识点较多,综合性较强,运算量大,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
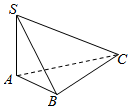 如图,三棱锥S-ABC中,SA⊥平面ABC,AB=6,BC=12,AC=6$\sqrt{5}$.SB=6$\sqrt{2}$,则三棱锥S-ABC外接球的表面积为216π.
如图,三棱锥S-ABC中,SA⊥平面ABC,AB=6,BC=12,AC=6$\sqrt{5}$.SB=6$\sqrt{2}$,则三棱锥S-ABC外接球的表面积为216π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com