
分析 (Ⅰ)利用绝对值的几何意义,即可求f(x)≤3x的解集;
(Ⅱ)利用绝对值的几何意义,去掉绝对值,即可求f(x)+|x+1|≤1的解集.
解答 解:(Ⅰ)由f(x)≤3x得①$\left\{{\begin{array}{l}{2x-1≥0}\\{2x-1≤3x}\end{array}}\right.$或②$\left\{{\begin{array}{l}{2x-1≤0}\\{1-2x≤3x}\end{array}}\right.$
解①得$x≥\frac{1}{2}$,解②得$\frac{1}{5}≤x<\frac{1}{2}$.
∴f(x)≤3x的解集为$\left\{{x\left|{x≥\frac{1}{5}}\right.}\right\}$.
(Ⅱ)f(x)+|x+1|≤1即|2x-1|+|x+1|≤1.
当$x≥\frac{1}{2}$时,不等式为2x-1+x+1≤1,解得$x≤\frac{1}{3}$,∴解集为空集;
当$-1<x<\frac{1}{2}$,不等式为-2x+1+x+1≤1,解得x≥1,∴解集为空集;
当x≤-1时,不等式为-2x+1-x-1≤1,∴解集为空集.
综上所述,x的取值范围为空集.
点评 本题考查不等式的解法,考查绝对值的几何意义,考查学生分析解决问题的能力,属于中档题.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:选择题
| A. | m=13,n=20 | B. | m=14,n=20 | C. | m=20,n=20 | D. | m=20,n=30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,e${\;}^{\frac{1}{e}}}$) | B. | (1,e] | C. | (1,e2) | D. | (e${\;}^{\frac{1}{e}}}$,e2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
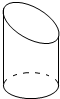 如图,一个底面半径为R的圆柱被与底面成30°二面角的平面所截,截面是一个椭圆,则该椭圆的焦距是( )
如图,一个底面半径为R的圆柱被与底面成30°二面角的平面所截,截面是一个椭圆,则该椭圆的焦距是( )| A. | R | B. | 2R | C. | $\frac{{\sqrt{3}}}{3}$R | D. | $\frac{{2\sqrt{3}}}{3}$R |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com