
 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第7幅图的蜂巢总数为( )
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第7幅图的蜂巢总数为( )| A. | 61 | B. | 90 | C. | 91 | D. | 127 |
分析 根据图象的规律可得相邻两项的差的规律可分析得出f(n)-f(n-1)=6(n-1),进而根据合并求和的方法求得f(n)的表达式,问题得以解决.
解答 解:由于f(2)-f(1)=7-1=6,
f(3)-f(2)=19-7=2×6,
f(4)-f(3)=37-19=3×6,
f(5)-f(4)=61-37=4×6,…
因此,当n≥2时,有f(n)-f(n-1)=6(n-1),
所以f(n)=[f(n)-f(n-1)]+[f(n-1)-f(n-2)]+…+[f(2)-f(1)]+f(1)=6[(n-1)+(n-2)+…+2+1]+1=3n2-3n+1.
又f(1)=1=3×12-3×1+1,
所以f(n)=3n2-3n+1.
当n=7时,f(7)=3×72-3×7+1=127.
故选:D.
点评 本题主要考查了数列的问题、归纳推理.属于基础题.


科目:高中数学 来源: 题型:填空题
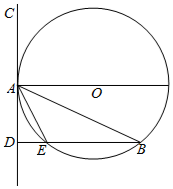 如图,在⊙O中,AB是弦,AC是⊙O的切线,A是切点,过B点作BD⊥AC于D,BD交⊙O于E点,若AE平分∠BAD,则∠BAD=60°.
如图,在⊙O中,AB是弦,AC是⊙O的切线,A是切点,过B点作BD⊥AC于D,BD交⊙O于E点,若AE平分∠BAD,则∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰直角三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.
已知多面体ABCDEF如图所示,其中ABCD为矩形,△DAE为等腰直角三角形,DA⊥AE,四边形AEFB为梯形,且AE∥BF,∠ABF=90°,AB=BF=2AE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=13,n=20 | B. | m=14,n=20 | C. | m=20,n=20 | D. | m=20,n=30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com