
分析 由圆的方程求出圆心坐标,由题意将圆心坐标代入直线方程化简,由“1”的代换和基本不等式求出答案.
解答 解:圆x2+y2-2x+4y+1=0的圆心坐标是(1,-2),
∵此圆关于直线2ax-by-2=0(a>0,b>0)对称,
∴直线过圆心,则2a+2b-2=0,即a+b=1,
∴$\frac{9}{a}+\frac{1}{b}$=(a+b)($\frac{9}{a}+\frac{1}{b}$)=10+$\frac{a}{b}+\frac{9b}{a}$≥10+2$\sqrt{\frac{a}{b}•\frac{9b}{a}}$=16,当且仅当$\frac{a}{b}=\frac{9b}{a}$时取等号,
∴$\frac{a}{b}+\frac{9b}{a}$的最小值是16,
故答案为:16.
点评 本题考查了直线与圆的位置关系,“1”的代换,基本不等式求最值问题,考查化简、变形能力.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
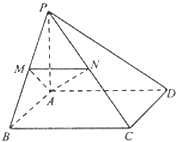 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M,N分别为线段PB,PC 上的点,MN⊥PB.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M,N分别为线段PB,PC 上的点,MN⊥PB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com