
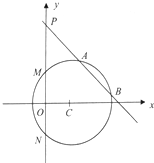
 已知圆心在x轴正半轴上的圆C与直线5x+12y+21=0相切,与y轴交于M,N两点,且∠MCN=120°.
已知圆心在x轴正半轴上的圆C与直线5x+12y+21=0相切,与y轴交于M,N两点,且∠MCN=120°.分析 (1)设圆C的方程为(x-a)2+y2=4a2,利用点C到直线5x+12y+21=0的距离为$d=\frac{|5a+21|}{13}=2a$,求出a,即可求圆C的标准方程;
(2)利用△MNG的面积为$\sqrt{3}$,得出|xG|=1,设A(x1,y1),B(x2,y2),则${x_G}=\frac{{{x_1}+{x_2}+0}}{3}$,即x1+x2=3xG,直线方程与圆的方程联立,即可得出结论.
解答 解:(1)由题意知圆心C(a,0),且a>0,
由∠MCN=120°知Rt△MCO中,∠MCO=60°,|OC|=a,则|CM|=2a,
于是可设圆C的方程为(x-a)2+y2=4a2
又点C到直线5x+12y+21=0的距离为$d=\frac{|5a+21|}{13}=2a$,
所以a=1或$a=-\frac{21}{31}$(舍),
故圆C的方程为(x-1)2+y2=4.
(2)△MNG的面积$S=\frac{1}{2}|MN||{x_G}|=\sqrt{3}|{x_G}|=\sqrt{3}$,
所以|xG|=1,
若设A(x1,y1),B(x2,y2),则${x_G}=\frac{{{x_1}+{x_2}+0}}{3}$,即x1+x2=3xG,
当直线l斜率不存在时,△ABO不存在,
故可设直线l为y=kx+2,代入圆C的方程(x-1)2+y2=4中,可得(1+k2)x2+(4k-2)x+1=0,
则$\left\{{\begin{array}{l}{(1+{k^2}){x^2}+(4k-2)x+1=0}\\{△>0⇒k<0或k>\frac{4}{3}}\\{{x_1}+{x_2}=\frac{2-4k}{{1+{k^2}}}}\end{array}}\right.$
所以$\frac{2-4k}{{1+{k^2}}}=3$或$\frac{2-4k}{{1+{k^2}}}=-3$
得k=-1或$k=-\frac{1}{3}$,
故满足条件的直线l的方程为y=-x+2或$y=-\frac{1}{3}x+2$.
点评 本题考查圆的方程,考查直线与圆的位置关系,考查韦达定理的运用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{1+\sqrt{2}}}{4}$ | B. | $\frac{{1-\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{3}+\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{3}-\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{2\sqrt{10}}}{5}$ | D. | $-\frac{{2\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | 10 | 27 | 37 |
| 不赞成 | 10 | 3 | 13 |
| 合计 | 20 | 30 | 50 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 19 | C. | 20 | D. | 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com