
| A. | 18 | B. | 19 | C. | 20 | D. | 21 |
分析 根据黑点和圈的排列规律,即可确定前233个圈中的●的个数.
解答 解:根据题意,将圆分组:
第一组:○●,有2个圆;
第二组:○○●,有3个圆;
第三组:○○○●,有4个圆;
…
每组的最后为一个实心圆;
每组圆的总个数构成了一个等差数列,前n组圆的总个数为s=(1+2+3+…+n)+n=$\frac{n(n+1)}{2}$+n=$\frac{n(n+3)}{2}$≤233,
∴n(n+3)≤466
∴n=17时,17×20=340,
当n=18时,18×21=378,
当n=19时,19×22=418,
当n=20时,20×23=460,
当n=21时,21×24=504>466,
∴n=20.
故选:C.
点评 本题主要考查归纳推理的应用,利用数列求和的知识是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
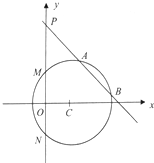 已知圆心在x轴正半轴上的圆C与直线5x+12y+21=0相切,与y轴交于M,N两点,且∠MCN=120°.
已知圆心在x轴正半轴上的圆C与直线5x+12y+21=0相切,与y轴交于M,N两点,且∠MCN=120°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com